Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 5.Problemas - Ex. 33

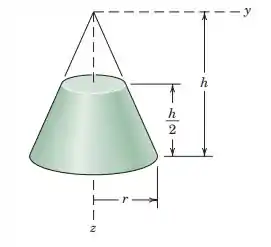
5.33. Calculate the distance measured from the base to the centroid of the volume of the frustum of the right-circular cone.

Passo 1

Vamos lá, queremos descobrir o centro de massa no eixo y , e para isso vamos usar a equação

y - = ∫ y c d V V

Primeiro vamos descobrir o elemento de área d V .

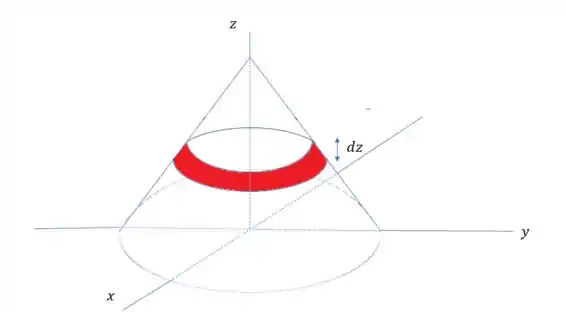
A gente pode aproximar isso para o volume de um cilindro com largura d z e raio ρ , mas olha só, esse raio vaira com a altura. A gente pode deduzir a relação do raio com a altura se pegarmos uma seção da imagem que forma um triângulo.

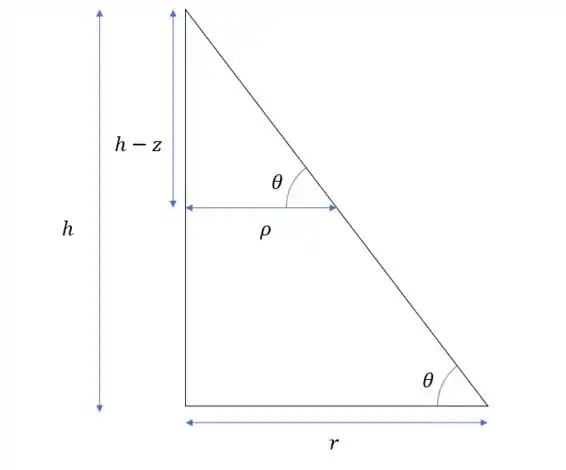
Por semelhança de triângulos podemos usar a relação

r h = ρ h - z

Então

ρ = h - z h ⋅ r

O elemento infinitesimal de volume então fica

d V = ρ 2 π ⋅ d z

Logo

d V = h - z h ⋅ r 2 π ⋅ d z

E nessa imagem temos

z c = z

Esse problema aqui tem uma simetria interessante para a gente, porque ele é totalmente simétrico no plano x y , então

x - = y - = 0

Passo 2

Beleza, agora vamos determinar o volume do nosso sólido, para isso é só usar a integral

V = ∫ d V

Então

V = ∫ V h - z h ⋅ r 2 π ⋅ d z

Os limites a gente vê imediatamente na imagem

V = ∫ 0 h 2 h - z h ⋅ r 2 π ⋅ d z

Isso fica

V = ∫ 0 h 2 h - z 2 h 2 r 2 π ⋅ d z

Vamos tirar as constantes da integral

V = r 2 π h 2 ∫ 0 h 2 h - z 2   d z

Então

V = r 2 π h 2 ∫ 0 h 2 h 2 + z 2 - 2 h z d z

Temos

V = r 2 π h 2 h 2 z + z 3 3 - h z 2 0 h 2

V = r 2 π h 2 h 3 2 + h 3 24 - h 3 4

E finalmente ficamos com

V = r 2 π h 2 ⋅ 7 24 h 3 = 7 24 r 2 π h

Passo 3

Agora vamos finalmente usar a integral para descobrir a coordenada de z do centro de massa.

z - = ∫ 0 h 2 z V d V

Substituindo V e d V

z - = 24 7 r 2 π h ∫ 0 h 2 z h - z h ⋅ r 2 π   d z

Isso aqui fica

z - = 24 7 r 2 π h ∫ 0 h 2 z h - z 2 h 2 r 2 π   d z

Tirando as constantes

z - = 24 7 r 2 π h ⋅ r 2 π h 2 ∫ 0 h 2 z h - z 2   d z

E a gente pode simplificar para

z - = 24 7 h 3 ⋅ ∫ 0 h 2 z h 2 + z 3 - 2 h z 2   d z

E aí temos

z - = 24 7 h 3 ⋅ z 2 h 2 2 + z 4 4 - 2 3 h z 3 0 h 2

Resolvendo isso

z - = 24 7 h 3 ⋅ h 4 8 + h 4 64 - h 4 12

Agora vamos chegar no resultado:

z - = 11 56 h

Resposta

z - = 11 56 h

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

5.47. Determine the x- and y-coordinates of the centroid of the shaded area.
5.50. Determine the y-coordinate of the centroid of the shaded area.
5.4748. Determine the coordinates of the centroid of the shaded area.
5.41. Determine the y-coordinate of the centroid of the plane area shown. Set h = 0 in your result and compare with the result y - = 4 a 3 π for a full semicircular area (see Sample Problem 5/3 and Ta
5.58. Determine the coordinates of the mass center of the body which is constructed of three pieces of uniform thin plate welded together.