Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 5.Problemas - Ex. 58
5.58. Determine the coordinates of the mass center of the body which is constructed of three pieces of uniform thin plate welded together.
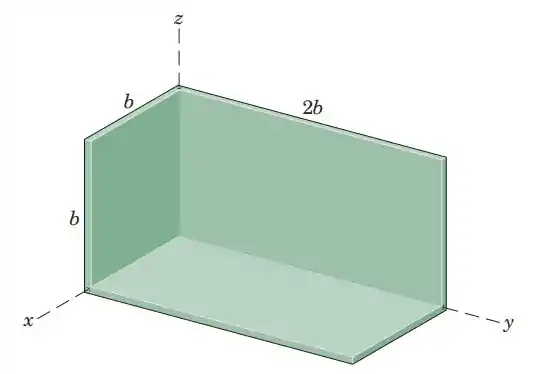
Passo 1
Vamos em busca de mais um centroide!
Essa figura é um pouco complicada para calcular o centroide, por isso vamos separar em várias figuras mais fáceis de calcular:
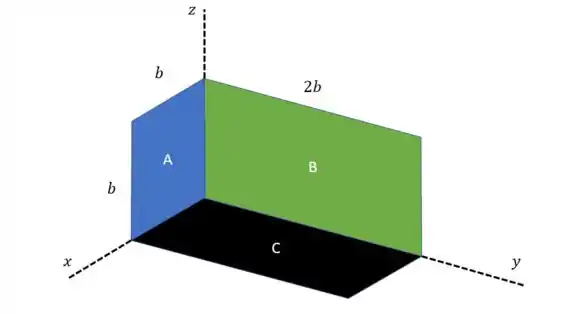
Então vamos dividir em três retângulos, cada um sendo uma face de uma caixa.
Passo 2
Podemos começar com o retângulo A, em azul.
E o centroide dessa figura fica o seguinte
E como a figura está no plano , temos
Passo 3
Vamos para o retângulo, B, que está em verde.
E vamos ver como fica a componente do centroide desse retângulo.
E
Passo 4
E finalmente o retângulo C, que está em preto.
E as componentes do centroide:
E
Passo 5
Agora vamos calcular o centroide da figura completa. Começando pela componente .
Isso fica
Substituindo esses valores
Então
Passo 6
Agora vamos fazer a mesma coisa em .
Isso fica
Substituindo esses valores
Então
Passo 7
Agora só falta para o eixo .
Isso fica
Substituindo esses valores
Então
E terminamos mais um problema.