Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 5.Problemas - Ex. 61

5.61. Determine the coordinates of the center of mass of the bracket, which is made from a plate of uniform thickness.

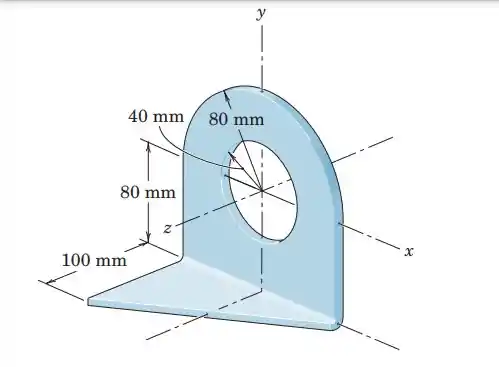
Passo 1

Beleza, vamos fragmentar o problema

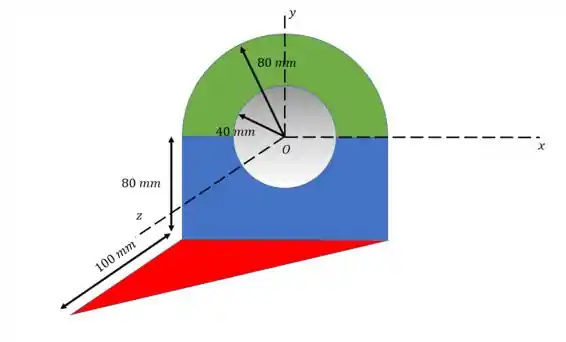
Então temos 4 figuras: o triângulo vermelho, o retângulo azul, o semicírculo verde e o círculo branco, atenção ao círculo, que é uma parte que falta na figura, então seus resultados são negativos. A gente pode considerar a origem do sistema de coordenadas no centro do círculo.

Passo 2

Podemos começar com o retângulo azul. Vamos começar com a área. Bom, sua altura está explicita na figura, e sua base é duas vezes o raio do semicírculo, então

A 1 = b ⋅ h = 2 80 ⋅ 80 = 12800   m m 2

E agora vamos determinar seu centroide, começando pelo eixo x , olha só, o centro   O está exatamente no centro do retângulo, então

x - 1 = 0

Agora vamos para o eixo y .

y - 1 = - 80 2 = - 40   m m

E essa figura está contida somente no plano x y , então

z - 1 = 0

Passo 3

Vamos para o semicírculo verde. Sua área é:

A 2 = 1 2 π r 2 = 1 2 π 80 2 ≈ 10053   m m 2

Agora vamos para o centroide. Assim como o retângulo, a origem O está exatamente no centro do semicírculo ao longo do eixo x , e está contida somente no plano x y , então:

x - 2 = 0

z - 2 = 0

E agora vamos calcular para y

y - 2 = 4 3 r π = 4 3 80 3 = 33,95   m m

Passo 4

É a hora do círculo, sua área fica:

A 3 = - π r 2 = - π 40 2 = - 5026,5   m m 2

Calcular o centroide dessa figura é muito simples, o círculo é uma figura perfeitamente simétrica, então o centroide é exatamente no centro da figura, e o centro da figura está no mesmo ponto que a origem O , então:

x - 3 = y - 3 = z - 3 = 0

Passo 5

Agora só falta o triângulo vermelho.

A 4 = b ⋅ h 2 = 100 ⋅ 2 80 2 = 8000   m m 2

Agora vamos para o centroide, e para isso vamos mudar um pouco nosso sistema de coordenadas.

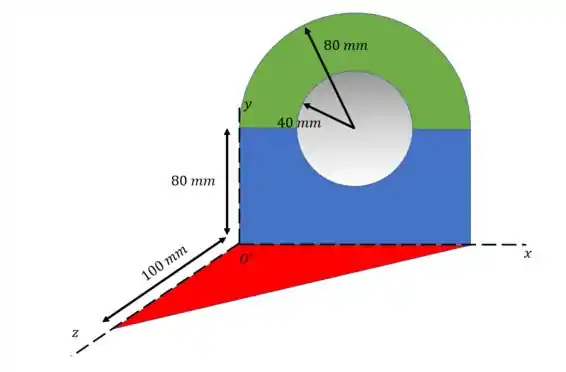
Agora a origem O ' está no ponto - 80 ;   - 80 ; 0

Vamos começar com o centroide em x

x - 4 ' = b 3 = 2 ( 80 ) 3 = 53,33   m m

Agora vamos fazer para z

z - 4 ' = h 3 = 100 3 = 33,33   m m

Agora vamos passar isso para o sistema original de coordenadas:

x - 4 = x - 4 ' + O '

Logo

x - 4 = 53,33 - 80 = - 26,67   m m

E

z - 4 = z - 4 ' + O '

Então

z - 4 = 33,33 + 0 = 33,33   m m

E como esse triângulo está no plano x z :

y - 4 ' = 0

Então

y - 4 = 0 - 80 = - 80   m m

Passo 6

Agora vamos calcular o centroide da figura toda:

x - = ∑ A x - ∑ A

Isso fica

x - = 12800 ⋅ 0 + 10053 ⋅ 0 - 5026,5 ⋅ 0 + 8000 ⋅ - 26,67 12800 + 10053 - 5027 + 8000 = - 8,26   m m

Agora vamos fazer para y - :

y - = ∑ A y - ∑ A

Isso fica

y - = 12800 ⋅ - 40 + 10053 ⋅ 33,95 - 5026,5 ⋅ 0 + 8000 ⋅ - 80 12800 + 10053 - 5027 + 8000 = - 31,39   m m

E finalmente

z - = ∑ A z - ∑ A

Isso fica

z - = 12800 ⋅ 0 + 10053 ⋅ 0 - 5026,5 ⋅ 0 + 8000 ⋅ 33,33 12800 + 10053 - 5027 + 8000 = 10,32   m m

E terminamos mais um problema.

Resposta

x - = - 8,26   m m y - = - 31,39   m m z - = 10,32   m m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Localize o centroide do quarto de cone.
Localize o centroide do sólido.
Localize o centroide do elipsoide de revolução.
Localize o centroide z do volume.
Determine o centróide da em z da figura abaixo.