Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 5.Problemas - Ex. 36
5.36. Os pés A e B são usados para estabilizar o guindaste para que não tombe ao levantar grandes cargas. Se a carga a ser suspensa é , determine o ângulo máximo da lança de modo que o guindaste não tombe. O guindaste possui uma massa de e centro de massa em , enquanto a lança tem uma massa de e centro de massa em .
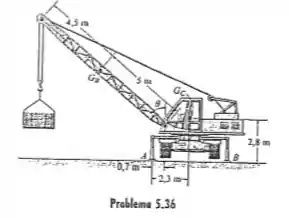
Passo 1
Fala galerinha, bora resolver essa parada. O problema quer o máximo ângulo para que o guindaste não tombe, aqui a gente precisa trabalhar com equilíbrio então precisamos de um belo desenho, mostrando onde cada força vai atuar.
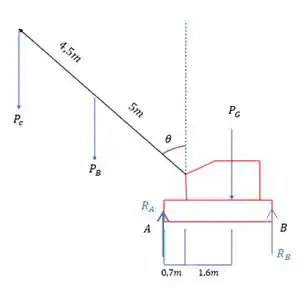
Lembrando que para calcular os pesos a gente faz:
O peso da carga:
O peso da barra:
E por fim:
O peso do guindaste:
Passo 2
Agora que a gente tem todo mundo, vamos escolher um bom ponto para usar a equação do somatório dos momentos. De qualquer maneira vamos precisar decompor o comprimento da barra pra horizontal já que as forças são verticais.
Para o guindaste ficar na iminência de tombar as reações no apoio B precisam ser zero e nesse caso vale a pena que escolhamos o ponto A para eliminar incógnitas.
Pela direita de A, temos o peso do guindaste que gera:
Pela esquerda, vamos precisar decompor a barra pra horizontal:
A distância horizontal até o centro da barra vai ser:
E até a carga vai ser:
E os momentos serão no sentido anti-horário:
Enfim podemos calcular o somatório dos momentos em C.
Considerando o sentido anti-horário positivo:
*