Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.3 - Ex. 43
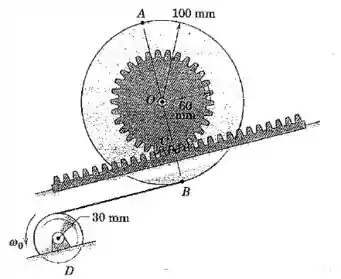
O movimento do volante enquanto rola para cima a cremalheira fixa sobre o seu núcleo dentado é controlado por meio do cabo periférico pela roda motora , que gira no sentido anti-horário na taxa constante durante um curto intervalo de movimento. Examinando a geometria de uma pequena rotação (diferencial) da linha enquanto gira instantaneamente em torno do ponto de contato , determine a velocidade angular do volante e as velocidades do ponto e do centro . Encontre também a aceleração do ponto .
Passo 1
Vamos seguir a sugestão do enunciado: analisar uma rotação diferencial em torno do ponto de contato , e vamos fazer isso usando o método que o livro oferece.
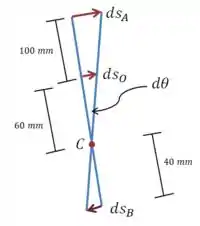
Esse diagrama representa alguns deslocamentos muito pequenos de pontos do volante e da engrenagem:
Já sabemos que o movimento do volante é gerado pelo enrolamento do fio em torno do pequeno disco que gira com e raio , então:
Passo 2
Agora vamos usar o diagrama para explorar as relações entre os pontos.
E então:
Agora queremos as velocidades dos pontos e :
Passo 3
E agora falta encontrar a aceleração no ponto . Considerando que a velocidade de enrolamento do fio que move a engrenagem é constante, podemos garantir que a única aceleração em é centrípeta, então:
E nesse caso usamos o raio como porque precisamos considerar a distância entre o ponto e o centro de sua trajetória circular.
Resposta
, , e .