Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 8.Problemas de Revisão - Ex. 68

τ a d m = 55 M P a   e considerando que são transmitidos 8 k W   na engrenagem F e 12kW na engrenagem G, determine o menor diâmetro admissível para o eixo AB.

Passo 1

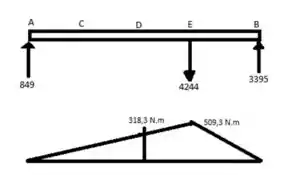
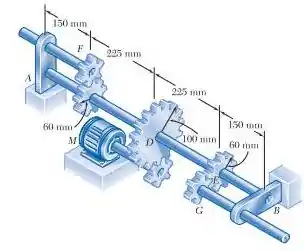
E ai gurizada tudo certo? O enunciado pede para que a gente determine o menor diâmetro admissível para o eixo AB. Para isso vamos esboçar o diagrama de corpo livre :D

Temos que a frequência é de:

f = 450 60 = 7,5 H z

Passo 2

Agora vem comigo determinar os torques nas seções ;)

Torque aplicado no D:

T D = P 2 π f = 20 × 10 3 2 π 7,5 = 424,41 N ∙ m

Torque nas engrenagens C e E:

T c = 8 20 T D = 169,76 N ∙ m

T E = 12 20 T D = 254,65 N ∙ m  

Passo 3

Continuamos, nãoo desistam de mim

Força nas engrenagens:

F D = T D r D = 424,41 100 × 10 - 3 = 4244 N

F C = T C r C = 169,76 60 × 10 - 3 = 2829 N

F E = T E r E = 254,65 60 × 10 - 3 = 4244 N

Torque em várias partes.

A C : T = 0

C D : T = 169,76 N ∙ m

D E : T = 254,65 N ∙ m

E B : T = 0

Passo 4

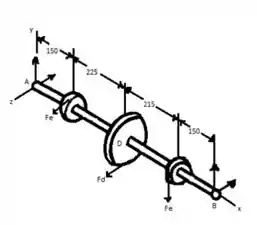
Consideremos o esboço abaixo para determinarmos o momento ;)

Ponto crítico:

T = 254,65 ∙ m

M y = 1007,9 N ∙ m

M z = 318,3 N ∙ m

M y 2 + M z 2 + T 2 m a x = 1087,2 N ∙ m

τ a l l = c J M y 2 + M z 2 + T 2 m a x

J c = π 2 c 3 = M y 2 + M z 2 + T 2 m a x τ a l l = 1087,2 55 × 10 6 = 19,767 × 10 - 3 m 3

c = 23,26 × 10 - 3 m

d = 2 c = 46,5 × 10 - 3 m   d = 46,5 m m

Forças no plano vertical

Resposta

d = 46,5 m m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A componente AB tem uma seção transversal retangular uniforme de 10×24m m . Para o carregamento mostrado, determine as tensões normal e de cisalhamento (a) no ponto H e (b) no ponto K.
A componente AB tem uma seção transversal retangular uniforme de 10mm x 24mm. Para o carregamento mostrado, determine as tensões normal e de cisalhamento (a) no ponto H e (b) no ponto K.
A componente AB tem uma seção transversal retangular uniforme de 10×24m m . Para o carregamento mostrado, determine as tensões normal e de cisalhamento (a) no ponto H e (b) no ponto K.
Uma força de 13kN é aplicada a coluna ABD com 60mm de diâmetro de ferro fundido conforme mostrado. No ponto H, determine (a) as tensões principais e os planos principais, (b) a tensão de cisalhamento
Três forças são aplicadas a uma placa com 101,6mm de diâmetro que está fixada a um eixo cheio AB de 45,7 mm de diâmetro. No ponto H, determine (a) as tensões e os planos principais e (b) a tensão de c