Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.3 - Ex. 50

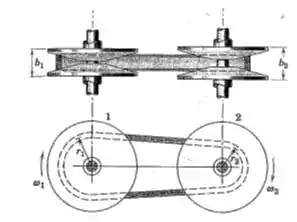
5/50) Uma transmissão por correia com velocidade variável consiste em duas polias , cada uma das quais constituída por dois cones que gram como uma unidade mas com capacidade de serem unidos ou separados de modo a variar o raio efetivo da polia . Se a velocidade angular ω 1 da polia 1 é constante , determine a expressão para a aceleração angular α 2 = ω 2 '   da polia 2 em termos das taxas de variação r 1 '   e r 2 ' dos raios efetivos .

Passo 1

Então galera , comos as duas polias então conectadas , sabemos que a velocidade tangencial em cada uma delas é a mesma . Sendo assim :

v 1 = v 2

r 1 ω 1 = r 2 ω 2

Derivando os dois lados para obtermos uma relação entre as acelerações angulares , obtemos que :

r 1 ' ω 1 + r 1 ω 1 ' = r 2 ' ω 2 + r 2 ω 2 '

Isolando ω 2 ' na equação , obtemos que :

ω 2 ' = r 1 ' ω 1 + r 1 ω 1 ' - r 2 ' ω 2 r 2

Logo , para ω 1 ' = 0 e α 2 = ω 2 ' , nós temos que :

α 2 = ω 2 ' = r 1 ' ω 1 - r 2 ' ω 2 r 2 = r 1 ' r 2 - r 1 r 2 ' r 2 2 ω 1  

Resposta

α 2 = r 1 ' r 2 - r 1 r 2 ' r 2 2 ω 1

Tranquilo pessoal? Então partiu resolver mais questões

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para o mecanismo do problema indicado nas figuras, determine a aceleração do colar B.
A barra AB de comprimento de 500 mm está conectada por juntasrotuladas aos colares A e B, que deslizam ao longo das duas barrasmostradas na figura. Sabendo que o colar B aproxima-se do ponto Ea uma ve
A barra AB de comprimento de 275 mm está conectada por juntasrotuladas aos colares A e B, que deslizam ao longo das duas barrasmostradas na figura. Sabendo que o colar B se move em direção auma veloci
Para o mecanismo do problema indicado nas figuras, determine a aceleração do colar A.
Um setor circular de uma placa de 45° com 250 mm de raio é preso a uma junta rotulada em O. Enquanto a aresta OA se desloca na superfície horizontal, a aresta OB de desloca ao longo da parede vertical