Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 15.Problemas - Ex. 201

Um setor circular de uma placa de 45° com 250 mm de raio é preso a uma junta rotulada em O. Enquanto a aresta OA se desloca na superfície horizontal, a aresta OB de desloca ao longo da parede vertical. Sabendo que o ponto A se desloca com velocidade constante de 1.500 mm/s, determine para a posição mostrada na figura (a) a velocidade angular da placa, (b) a velocidade do ponto B .

Passo 1

E ai gurizada tudo belezinha???

O A _ = 10   i n . s i n s i n   60 ° i + 10   i n . c o s c o s   60 °   k  

r A = O A _ = ( 8.6603   i n .   i + 5   i n . k

r B = O B _ = ( r B ) x i + ( r B ) y j

Passo 2

Produto escalar:

O A _ ∙   O B _ = O A O B s i n s i n   45 °  

( 8.6603 i + 5 k ) ∙ ( r B ) x i + r B ) y j = ( 10 ) ( 10 s i n s i n   45 °  

8.6603 ( r B ) x = 70.711                       (   r B ) x = 8.165   i n .

( r B ) y = O B 2 - ( r B ) x 2 = 10 2 - 8.165 2 ; ( r B ) y = 5.773   i n .

r B = 8.165   i n . i + 5.773   i n . j

Passo 3

Uma vez que v A é perpendicular a OA, v A forma 30 ° , ângulo com eixo.

v A = ( 60   i n . / s ) ( - s i n s i n   30 °   i + c o s c o s   60 °   j )

v A = - ( 30   i n . / s ) i + ( 51.96   i n / s ) k

Plano OAB: ω = ω x i + ω y j + ω z k

v A = ω × r A   :

- 30 i + 51.96 k = 5 ω y + 8.6603 ω z - 5 ω x j - 8.6603 ω y k

i :         - 30 = 5 ω y                               ω y = - 6   r a d / s

j :           0 = 8.6603 ω z               ω z = 0.57735 ω x

k :           51.96 = - 8.6603 ω y                     ω y = - 6   r a d / s

v B = ω × r B

Passo 4

v B = - 5.773 ω z i + 8.165 ω z j + 5.773 ω x - 8.165 ω y k

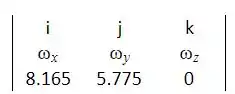
Uma vez que o ponto B se move no plano xy,

( v B ) c = 0 = 5.773 ω x - 8.165 ω y

0 = 5.773 ω x - 8.165 ( - 6 )

ω x = - 8.486   r a d / s

ω z = 0.57735 - 8.486 = - 4.899   r a d / s

Passo 5

( v B ) x = - 5.773 - 4.899 = 28.3   i n . / s

( v B ) y = 8.165 - 4.899 = - 40.0   i n . / s

( v B ) z = 0

Resposta

a) ω = - ( 8.48   r a d / s ) i - ( 6   r a d / s ) j - ( 4.90   r a d / s ) k

b) v B = ( 28.3   i n . / s ) i - ( 40.0   i n . / s ) j

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A barra AB está conectada por juntas rotuladas ao colar A e ao disco C de 400 mm de diâmetro. Sabendo que o disco C gira no sentido anti-horário à taxa constante ω 0 = 3 rad /s, no plano zx, determine
A barra AB de comprimento de 500 mm está conectada por juntasrotuladas aos colares A e B, que deslizam ao longo das duas barrasmostradas na figura. Sabendo que o colar B aproxima-se do ponto Ea uma ve
A barra AB de comprimento de 300 mm está conectada por juntas rotuladas aos colares A e B, que deslizam ao longo das duas barras mostradas na figura. Sabendo que o colar B aproxima-se do ponto D a uma
15.219. Mecanismo do Problema 15.207.
15.222. Para o mecanismo do problema indicado nas figuras, determine a aceleração do colar A.Mecanismo do Problema 15.206.