5.52. Três livros uniformes, cada um com peso W e comprimento , são empilhados como na figura. Determine a distância máxima que o livro do topo pode se projetar em relação ao da base, de modo que a pilha não tombe.

Cara, ele quer saber o valor de para o livro de cima não tombar. Percebe que livro de baixo não influencia a rotação dos de cima com seu peso. Apenas os livros de cima podem girar e tombar por causa do peso deles.

O livro de baixo só é um apoio para o segundo livro. Por isso a gente via ignorar ele, e só olhar para os dois livros de cima, que podem tombar por causa do seu peso.

Uma consideração importante é: quando o livro de cima cai, ele cai se seu centro de gravidade estiver à direita do ponto em que a metade dele já não esteja mais apoiado. Ou seja, se ele tiver um comprimento maior que não apoiado. Então daí, a gente tira que o espaçamento entre ele e livro de baixo é no máximo.

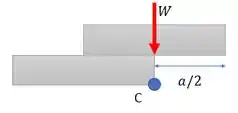
Percebe que se estiver mais para a direita, esse livro tomba por que não há mais reação para rotação causada por .

Cada livro tem largura e peso . Se a gente posicionar no centroide de cada livro. E pensar que o livro de baixo dá reações ao livro do meio nos contatos nas extremidades. Nosso DCL fica:

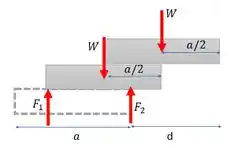
Na eminência de rodar todo o sistema desses dois livros, a reação é nula, e todo o sistema está parado. Ou seja, vale que o somatório de momento em qualquer ponto é zero. Inclusive no ponto onde temos reação . Aí a gente pode escrever:

Aí a gente vai usar essa equação para achar nosso valor de em função de e . Bora!