Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 5.Problemas - Ex. 18

Determine as coordenadas do centroide da área sombreada.

Passo 1

Fala galera, tudo certo? Bora fazer mais um exercício? Prometo que vai ser bem rapidinho!

O enunciado nos pede para determinar as coordenadas x - e y - do centroide da área sombreada.

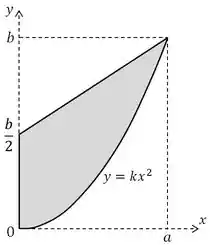
Então bora resolver! Lembrando que neste caso estamos lidando com uma área e as fórmulas gerais para determinar as coordenadas do centroide de uma área são:

x - = ∫ x c d A A

y - = ∫ y c d A A

Passo 2

Vamos começar então definindo a área da porção sombreada da figura, para isso vamos subtrair a equação da área interna da equação da área externa. Para a área interna temos:

y 1 = k x 2

Onde a constante k pode ser obtida pelo ponto ( a , b ) :

b = k a 2

k = b a 2

∴ y 1 = b a 2 x 2

E a reta que define área externa pelos pontos 0 , b 2 e a , b :

y 2 = b 2 a x + b 2

Logo, a equação da área sombreada é:

y = y 2 - y 1

y = b 2 a x + b 2 - b a 2 x 2

E a área total:

A = ∫ d A = ∫ 0 a y d x

A = ∫ 0 a b 2 a x + b 2 - b a 2 x 2 d x

A = b 4 a x 2 + b 2 x - b 3 a 2 x 3 0 a

A = a b 4 + a b 2 - a b 3

A = 5 a b 12

Passo 3

Show de bola! Feito isso, vamos analisar a porção infinitesimal destacada em vermelho:

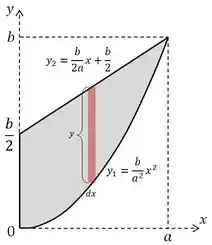
Onde a área infinitesimal é dada por:

d A = y d x

d A = y 2 - y 1 d x

Vamos começar pela coordenada x - do centroide. Para isso, temos que:

x c = x

Substituindo todos os termos na equação de x - do Passo 1, cujos limites de integração são ( 0 , a ) , temos:

x - = ∫ x c d A A

x - * A = ∫ 0 a x y 2 - y 1 d x

x - * A = ∫ 0 a x b 2 a x + b 2 - b a 2 x 2 d x

x - * A = ∫ 0 a b 2 a x 2 + b 2 x - b a 2 x 3 d x

x - * A = b x 3 6 a + b x 2 4 - b x 4 4 a 2 0 a

x - * A = b a 3 6 a + b a 2 4 - b a 4 4 a 2

x - = b a 2 6 * 12 5 a b

x - = 2 a 5

Passo 4

Ainda tem coisa pra fazer?

Olhando esse tanto de conta parece coisa de outro mundo, mas no final prometo que vai dar tudo certo. Bora continuar! Agora vamos analisar a coordenada y - do centroide. Onde:

y c = y 1 + y 2 2

Substituindo todos os termos na equação de y - do Passo 1, cujos limites de integração são ( 0 , a ) , temos:

y - = ∫ y c d A A

y - * A = ∫ 0 a y 1 + y 2 2 y 2 - y 1 d x

y - * A = 1 2 ∫ 0 a y 2 2 - y 1 2 d x

y - * A = 1 2 ∫ 0 a b 2 a x + b 2 2 - b a 2 x 2 2 d x

y - * A = 1 2 ∫ 0 a b 2 4 a 2 x 2 + b 2 2 a x + b 2 4 - b 2 a 4 x 4 d x

y - * A = 1 2 b 2 12 a 2 x 3 + b 2 4 a x 2 + b 2 4 x - b 2 5 a 4 x 5 0 a

y - * A = 1 2 b 2 12 a 2 a 3 + b 2 4 a a 2 + b 2 4 a - b 2 5 a 4 a 5

y - * A = 1 2 * a b 2 12 + a b 2 4 + a b 2 4 - a b 2 5

y - = 1 2 * 23 a b 2 60 * 12 5 a b

y - = 23 b 50

É isso, galera. Partiu pra próxima!

Resposta

x - = 2 a 5

y - = 23 b 50

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Localize o centroide y - da área.
A placa tem uma espessura de 12 mm e é composta de aço com um peso específico de 80 kN/m³. Determine as componentes horizontal e vertical da reação no pino A e a força na corda em B .
Localize o centroide da área. Dica: Escolha elementos de espessura d y e comprimento [ 2 - y - y 2 ] .
Localize o centroide ( x - ,y - ) da área.
Determine a área e o centroide ( x - ,y - ) da área.