Enunciado
Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 9.Problemas - Ex. 3
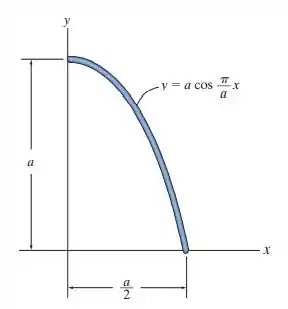
Localize o centroide do elemento uniforme. Calcule as integrais usando um método numérico.
Passo 1
Fala aí, galerinha do Responde aí. Tudo beleza? Vamos fazer mais uma questão de Estática.
Para determinarmos o centro de massa deste elemento homogêneo, devemos determinar a posição do elemento diferencial.
Neste caso, o elemento difrencial se encontra sobre a curva, em um ponto arbitrário . Podemos escrever seu comprimento em termos de e pelo teorema de pitágoras. Fica assim:
Em seguida, devemos substituir a derivada que encontramos na relação para o . Ela é dada por:
Primeiro, vamos determinar o numerador desta relação:
Integrando:
E para o denominador, temos:
Assim vai ser:
Passo 2
Agora, para determinarmos a posição do centro de massa, podemos utilizar vamos utilizar a seguinte relação:
Já temos o denominador, então bora determinar o numerador:
Logo, temos que vai ser:
É isso, galera, Bora resolver mais questões pra ficar craque.