Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.3 - Ex. 44
Desenvolva uma expressão para a velocidade de subida do mecanismo de elevação de veículos em termos de . A haste do pistão do cilindro hidráulico está se estendendo na taxa .
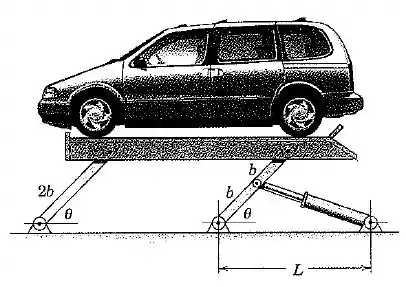
Passo 1
O enunciado deu a taxa com que o cilindro se expande, então nossa primeira tarefa é relacionar essa taxa com as outras grandezas do problema.
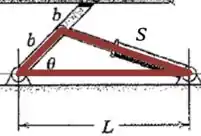
Vamos aplicar a lei dos cossenos nesse problema:
E derivando isso em relação ao tempo (lembrando que e são constantes):
Mas nosso objetivo é encontrar uma função que dê a velocidade de subida da plataforma.
Passo 2
Dê uma olhada na haste da esquerda, podemos aproveitar aquele ângulo para escrever uma relação que dá a altura da plataforma:
E derivando em relação ao tempo:
E podemos usar a fórmula que encontramos no passo para substituir nessa equação:
E então:
E é justamente a velocidade que queremos encontrar:
E só precisamos substituir a expressão para que encontramos lá em cima:
E então:
Resposta
A velocidade de elevação da plataforma é .