Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 5.Problemas - Ex. 58

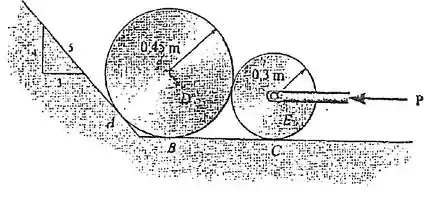
5.58. Os discos lisos D e E possuem um peso de 1   k N e 0,5   k N , respectivamente. Determine a maior força horizontal P que pode ser aplicada ao centro do disco E sem fazer o disco D subir a rampa.

Passo 1

Cara, ele quer o maior valor de P para essa situação ficar parada. Ou seja, em equilíbrio, tendo em vista a influencia da geometria do problema e o peso desses discos.

Pois bem, o jeito é a gente analisar disco por disco e ir criando relações entre as grandezas até chegar em P .

Vamos começar pelo DCL do disco E:

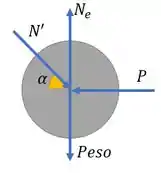
Temos o peso do disco que vai ser 0,5 kN, temos a força P , temos a normal que o disco faz com a superfície horizontal e a normal de contato com o disco D. Repara que ela é inclinada porque a sua linha de ação é a linha que liga os centros dos círculos.

E aí temos as equações de equilíbrio

F R x = 0

F R x = - P + N ' ⋅ cos ⁡ α = 0

Para achar esse cosseno podemos olhar a geometria do problema

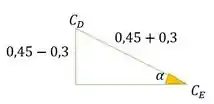
Onde C D é o centro de D e C E o centro de E.

cos ⁡ α = 0,75 2 - 0,15 2 0,75

Então

P = N ' 0,75 0,75 2 - 0,15 2     ( 1 )

E para y temos

F R y = 0

F R y = N c - 0,5 - N ' ⋅ sin ⁡ α = 0

Então

N c = 0,5 + N ' ⋅ 0,15 0,75       ( 2 )

Passo 2

Para o disco D temos

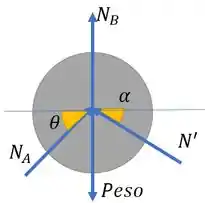
Onde N A e N B são as normais em relação as duas superfícies que ele está em contato.

F R x = 0

F R x = N A ⋅ cos ⁡ θ - N ' cos ⁡ α = 0

F R x = N A ⋅ cos ⁡ θ - N ' 0,75 2 - 0,15 2 0,75 = 0

Podemos determinar cos ⁡ θ   pela orientação da parede inclinada ao lado esquerdo de D. A figura diz que ela possui a inclinação de um triângulo 3/4/5. Nosso θ aparece entre o cateto de 4 e a hipotenusa. E para ele temos:

cos ⁡ θ = 4 5

N A ⋅ 4 5 = N ' 0,75 2 - 0,15 2 0,75   ( 3 )

E para y temos

F R y = 0

F R y = N A ⋅ sin ⁡ θ + N B - 1 + N ' ⋅ sin ⁡ α = 0

Então

N B = - N A ⋅ sin ⁡ θ + 1 - N ' ⋅ sin ⁡ α

N B = - N A ⋅ 3 5 + 1 - N ' ⋅ 0,15 0,75

Mas para P m á x requer N B = 0 , pois é a força limite onde o disco está quase rolando, então a força normal é nula.

Passo 3

Agora podemos resolver

0 = - N A ⋅ 3 5 + 1 - N ' ⋅ 0,15 0,75

0 = - N A ⋅ 3 5 + 1 - N ' ⋅ 1 5

Então

N A = 5 3 - N ' ⋅ 1 3

Substituindo em (3)

5 3 - N ' ⋅ 1 3 = N ' 0,75 2 - 0,15 2 0,75

Isolando N’

5 3 1 3 + 0,75 2 - 0,15 2 0,75 = N '

Então

N ' ≈ 1 , 27

Agora podemos determinar P, através da equação (1)

P = N ' ⋅ 0,75 2 - 0,15 2 0,75 ≈ 1 , 24   k N    

N C através de (2)

N c = 0,5 + 1,24 ⋅ 1 5 = 0 , 748   k N

E N A através de (3)

N A = 1,24 ⋅ 0,75 2 - 0,15 2 0,75 = 1,21   k N

Resposta

P = 1 , 24   k N    

N c = 0 , 748   k N

N A = 1,21   k N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A ferramente mostrada é usada para endireitar peças torcidas ao final de uma montagem com madeira. Se a força P = 150N é aplicada ao cabo como mostrado, determine as forças normais aplicadas à garra n
Calcule o módulo da força suportada pelo pino em B no dispositivo em curva, carregado e apoiado como mostrado.
A acrobata de 50k g pedala seu monociclo sobre o cabo esticado, mas ligeiramente elástico. Se a deflexão no centro do vão de 18m vale 75m m , determine a força trativa no cabo. Despreze os efeitos dos
A barra uniforme de 5m e massa de 100k g é articulada em O e impedida de girar mais do que 30 ° no plano vertical pelo rolete fixo em A . Calcule o módulo da força total suportada pelo pino em O .
Os projetistas do trem de pouso de um avião desejam fazer com que as forças em ambos os eixos A B e C D atuem ao longo de seus respectivos comprimentos. Que ângulo θ eles devem especificar para o eixo