Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 8.Problemas - Ex. 3

8.3. Uma força horizontal P = 100   N é suficiente apenas para apenas impedir que a caixa deslize plano abaixo, e uma força horizontal P = 350   N é necessária só para empurrar a caixa plano acima. Determine o coeficiente de atrito estático entre o plano e a caixa, e encontre a massa da caixa.

Passo 1

Vamos começar desenhando os diagramas de corpo livre.

Para o primeiro caso

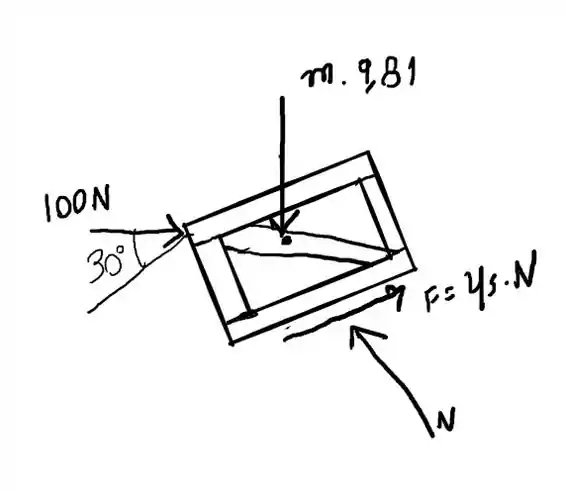
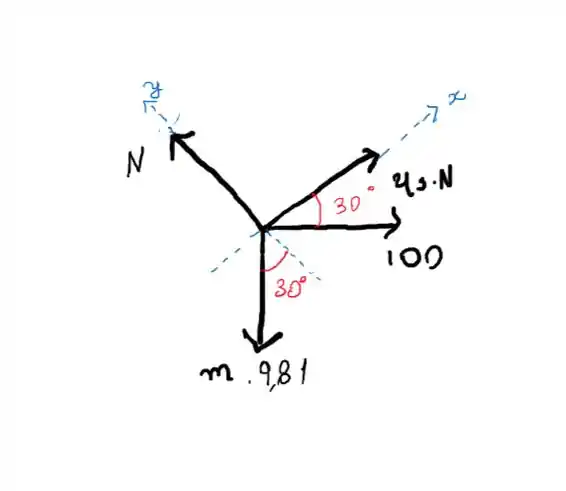
E para o segundo caso

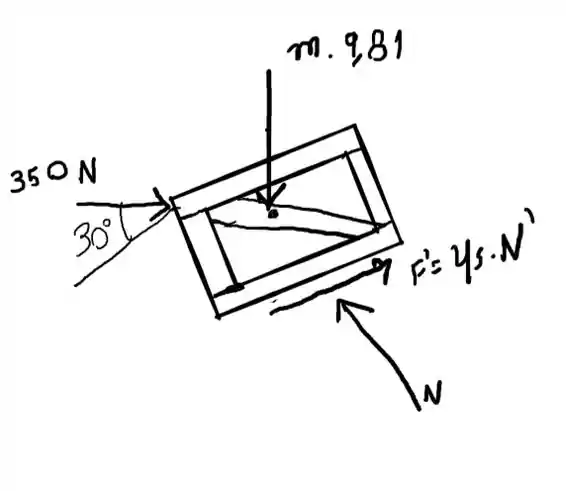
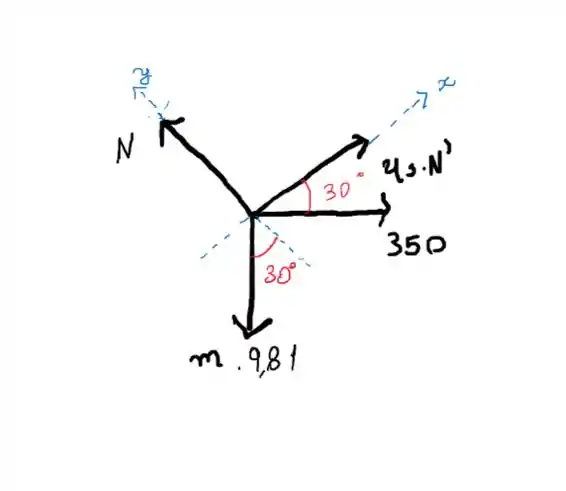
Passo 2

Agora vamos usar as equações de equilíbrio, para o primeiro caso temos

F R y = 0

F R y = N - 100 ⋅ sin ⁡ 30 ° - m ⋅ 9,81 ⋅ cos ⁡ 30 ° = 0

E para o eixo x

F R x = 0

F R x = μ s ⋅ N + 100 ⋅ cos ⁡ 30 ° - m ⋅ 9,81 ⋅ sin ⁡ 30 ° = 0

Isolando N na primeira equação

N = 100 ⋅ sin ⁡ 30 ° + m ⋅ 9,81 ⋅ cos ⁡ 30 °

E substituindo na segunda

μ s ⋅ ( 100 ⋅ sin ⁡ 30 ° + m ⋅ 9,81 ⋅ cos ⁡ 30 ° ) + 100 ⋅ cos ⁡ 30 ° - m ⋅ 9,81 ⋅ sin ⁡ 30 ° = 0

Agora vamos isolar μ s

μ s = m ⋅ 9,81 ⋅ sin ⁡ 30 ° - 100 ⋅ cos ⁡ 30 ° 100 ⋅ sin ⁡ 30 ° + m ⋅ 9,81 ⋅ cos ⁡ 30 ° = 4,905 ⋅ m - 86,603 8,496 ⋅ m + 50

Passo 3

Agora vamos usar as equações de equilíbrio para o segundo caso

F R y = 0

F R y = N ' - 350 ⋅ sin ⁡ 30 ° - m ⋅ 9,81 ⋅ cos ⁡ 30 ° = 0

E para o eixo x

F R x = 0

F R x = - μ s ⋅ N ' + 350 ⋅ cos ⁡ 30 ° - m ⋅ 9,81 ⋅ sin ⁡ 30 ° = 0

Isolando N na primeira equação

N ' = 350 ⋅ sin ⁡ 30 ° + m ⋅ 9,81 ⋅ cos ⁡ 30 °

E substituindo na segunda

- μ s ⋅ ( 350 ⋅ sin ⁡ 30 ° + m ⋅ 9,81 ⋅ cos ⁡ 30 ° ) + 350 ⋅ cos ⁡ 30 ° - m ⋅ 9,81 ⋅ sin ⁡ 30 ° = 0

Agora vamos isolar μ s

μ s = - m ⋅ 9,81 ⋅ sin ⁡ 30 ° - 350 ⋅ cos ⁡ 30 ° 350 ⋅ sin ⁡ 30 ° + m ⋅ 9,81 ⋅ cos ⁡ 30 ° = 303,11 - 4,905 ⋅ m 8,496 ⋅ m + 175

Passo 4

Agora podemos determinar m , pois sabemos que

μ s = 4,905 ⋅ m - 86,603 8,496 ⋅ m + 50

E

μ s = 303,11 - 4,905 ⋅ m 8,496 ⋅ m + 175

Então

4,905 ⋅ m - 86,603 8,496 ⋅ m + 50 = 303,11 - 4,905 ⋅ m 8,496 ⋅ m + 175

Isolando m

4,905 ⋅ m - 86,603 ⋅ 8,496 ⋅ m + 175 = 303,11 - 4,905 ⋅ m ⋅ 8,496 ⋅ m + 50

41,67 ⋅ m 2 + 122,596 ⋅ m - 15155,525 = - 41,67 ⋅ m 2 + 2329,972 ⋅ m + 15155,5

Isolando m

2 ⋅ 41,67 ⋅ m 2 + m ⋅ - 2329,972 + 122,596 - 15155,525 - 15155,5 = 0

Então

83,34 ⋅ m 2 - 2207,376 ⋅ m - 30311,025 = 0

Por bhaskaras

m = 36,57   k g

Logo

μ s = 4,905 ⋅ 36,57 - 86,603 8,496 ⋅ 36,57 + 50 = 0,256

Resposta

m = 36,57   k g μ s = 0,256

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Se os coeficientes de atrito estático nos pontos de contato A e B são μ s = 0 , 3 e μ s ' = 0 , 4 , respectivamente, determine a menor força P que fará com que o carrretel de 150k g tenha iminência de
Se o coeficiente de atrito estático entre os colares A e B e a barra é μ s = 0,6 , determine o ângulo máximo θ para o sistema permanecer em equilíbrio, independente do peso do cilindro D . As ligações
Cada um dos cilindros tem uma massa de 50k g . Se os coeficientes de atrito estático nos pontos de contato são μ A = 0,5 , μ B = 0,5 , μ C = 0,5 e μ D = 0,6 , determie o menor momento de binário M nec
Se θ = 15 ° , determine o menor coeficiente de atrito estático entre os colares A e B e a barra necessário para que o sistema permaneça em equilibrio, independente do peso do cilindro D . As ligações
Determine a menor força P que causará a iminência de movimento. A caixa e a roda têm uma massa de 50k g e 25k g , respectivamente. O coeficiente de atrito estático entre a caixa e o piso é μ s = 0 , 5