Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 7.8 - Ex. 64

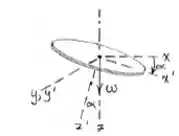
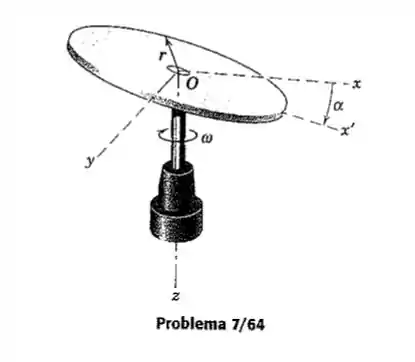
O disco circular de massa m e raio r está montado na haste vertical com um ângulo α entre seu plano e o plano de rotação da haste. Determine uma expressão para a quantidade de movimento angular H do disco em relação a O. Encontre o ângulo β que a quantidade de movimento angular H faz com a haste se α = 10 ° .

Passo 1

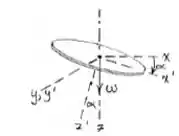
O primeiro passo é decompor a velocidade angular nos eixos x ´ - y ´ - z ´

Pela regra da mão direita nós teremos ω = ω k ^ decompondo no eixo x ´ utilizando α nós ficaremos com ω x ' = ω s e n ( α ) no eixo y ´ não teremos componente da velocidade angular assim ω y ' = 0 por fim em z ´ ω z ' = ω c o s ( α )

ω ' = ω c o s α k ^ + ω s e n ( α ) i   ̂

Agora a relação entre os versores :

i ^ ' = i ^ * cos ⁡ α + k ^ * s e n α

k ^ ' = - i ^ * sen ⁡ α + k ^ * c o s α

Passo 2

O eixo x ´ - y ´ - z ´ e o eixo de inércia principal para o disco por causa disso nós teremos somente o eixo da diagonal principal do tensor de inercia.

Note que por ser um disco I x ´ x ´ = I y ´ y ´ = 1 4 m r 2 tudo devido a sua simetria e que I z z = 1 2 m r 2

Passo 3

O nosso problema então se resume a equação 7/13

Onde H ' = I x ´ x ´ ω x ' i ^ ' + I y ´ y ´ ω y ' j ^ ' + I z z ω z ' k ^ '

Substituindo nós teremos

H ' = 1 4 m r 2 ω s e n α i ' ^ + 1 2 m r 2 ω c o s α k ^

H = 1 4 m r 2 ω s e n α i ^ * cos ⁡ α + k ^ * s e n α + 1 2 m r 2 ω c o s α ( = - i ^ * sen ⁡ α + k ^ * c o s α )

H = 1 4 m r 2 {   ( - s e n α cos ⁡ α i ^ + ( sin 2 ⁡ α + 2 cos 2 ⁡ α k ^ ) }

Onde α = 10 °

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O avião a jato tem uma massa de 22Mg e um centro de massa em G. Se um cabo de rebocar está fixado à parte superior do trem de pouso do nariz e exerce uma força T = 400N , como mostrado, determine a ac
A empilhadeira manual tem uma massa de 70 kg e centro de massa em G. Se ela levanta a bobina de 120 kg com uma aceleração de 3 m/s², determine as reações em cada uma das quatro rodas. A carga é simétr
O dragster tem uma massa de 1500 kg e um centro de massa em G. Se o coeficiente de atrito cinético entre as rodas traseiras e o pavimento é μ k = 0,6 , determine se é possível para o motorista levanta
O dragster tem uma massa de 1500 kg e um centro de massa em G. Se não ocorre nenhum deslizamento, determine a força de atrito F B que tem de ser desenvolvida em cada uma das rodas motrizes traseiras B
Na largada de uma corrida, as rodas motrizes traseiras B do carro de 775 kg derrapam na pista. Determine a aceleração do carro e a reação normal que a pista excerce sobre o par dianteiro de rodas A e