Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.9 - Ex. 198

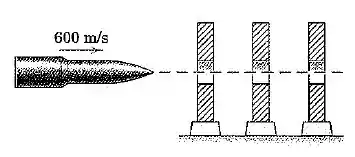
O projétil de 140   g é disparado com uma velocidade de 600   m / s e carrega três anilhas, cada uma com uma massa de 100   g . Encontre a velocidade comum v do projétil e das anilhas. Determine também a perda | ∆ E | de energia durante a interação.

Passo 1

Vamos aplicar a conservação do momento linear. Inicialmenete, quando o projétil viaja sozinho, o momento total do sistema é:

p i = M v 0 = 0,140 600 = 84   k g   m / s

E depois que o projétil passa a viajar junto com todas as três anilhas, o momento total do sistema é:

p f = 0,140 + 3 0,100   v = 0,440   v

Passo 2

Pela conservação de momento linear, podemos igualar essas duas expressões:

p i = p f

84 = 0,440   v

v ≅ 190,9   m / s

Passo 3

Agora para calcular a perda de energia é só fazer a diferença entre as energias cinéticas final e inicial:

E 0 = 1 2 M v 0 2 = 1 2 0,140 600 2 = 25   200   J

E f = 1 2 M + 3 m v 2 = 1 2 0,440 190,9 2 ≅ 8   017   J

E então a perda de energia é:

Δ E = 25200 - 8017 ≅ 17,2   .   10 3   J

Resposta

A velocidade comum é v = 190,9   m / s e a perda de energia é Δ E = 17,2   k J .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A bola de 2k g é lançada de modo a se mover horizontalmente a 10m / s quando atinge o bloco de 6k g , que está descendo o plano inclinado a 1m / s . Se o coeficiente de restituição entre a bola e o bl
Dois carros A e B têm massa de 2000k g e colidem no pavimento escorregadio de um cruzamento. A direção do movimento de carro após a colisão é medida pelos rastros deixados, como mostrado. Se o motoris
A bola de bilhar A move-se com uma velocidade de 10m / s imediatamente antes de atingir a bola B , que está em repouso. Se as massas de A e B são 200g cada e o coeficiente de restituição entre elas é
Dois discos A e B têm massas de 1k g e velocidades iniciais como mostrado imediatamente antes de colidirem. Se o coeficiente de restituição é e = 0,5 , determine suas velocidades escalares logo após o
Dois discos A e B têm massa de 1 5k g e 10k g , respectivamente. Se eles deslizam sobre um plano horizontal liso com as velocidades mostradas, determine suas velocidades escalares logo após o impacto.