Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 3.Problemas - Ex. 7

Uma força P de 49 N é aplicada em uma alavanca de câmbio. O momento P sobre B é horário e tem a intensidade de 28   N ⋅ m . Determine o valor de α .

Passo 1

Diagrama do corpo livre:

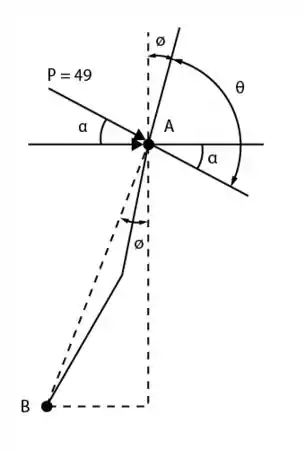
Passo 2

Sabemos que :

M B = r A / B ⋅ P s e n θ

Analisando o diagrama acima, podemos escrever:

θ = α + 90 - ϕ ϕ = arctan ⁡ 0,203 m 0,560   m = 19,92 º

Calculando a distância r A / B :

r A B 2 = 0,203   m 2 + 0,560   m 2 r A / B = 0,596   m

Passo 3

Substuituindo os valores:

M B = r A B ⋅ P s e n θ 28   N ⋅ m = 0,596   m ⋅ 49   N sen ⁡ α + 90 º - 19,92 º sen ⁡ α + 70,08 º = 0,959 α + 70,08 º = 73,563 º

Ou α + 70,08 º = 106,25 º α = 3,45 º

Resposta

α = 3,45 º

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um puxão T de 150N é dado em uma corda, que está firmemente enrolada na parte interna do tambor. Determine o momento de T em relação ao centro do tambor em C . Em que ângulo θ , T deve ser aplicado de
Elementos do braço são mostrados na figura. A massa do antebraço é de 2,3k g , com centro de massa em G . Determine o momento combinado em relação ao cotovelo em O dos pesos do antebraço e da esfera h
A força de 10N é aplicada sobre a manopla da válvula de controle hidráulico, como mostrado. Calcule o momento dessa força em relação ao ponto O .
Um praticante de exercício começa com seu braço na posição relaxada O A , na qual a fita elástica não está esticada. Ele então gira seu braço para a posição horizontal O B . O módulo elástico da fita
A força exercida pelo amortecedor A B sobre a porta vale 40N e está direcionada ao longo da linha A B . Esta força tende a manter a porta fechada. Calcule o momento desta força em relação à dobradiça