Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.7 - Ex. 166

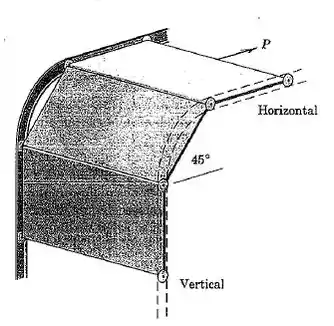
Cada um dos três painéis idênticos uniformes de uma porta industrial segmentada tem massa m e é conduzido nos trilhos (um mostrado em linha tracejada). Determine a aceleração horizontal a do no painel superior sob a ação da força P. Despreze qualquer atrito nos roletes de guia.

Passo 1

A partir do esquema disponível, é interessante a representação do diagrama dinâmico com as informações do sistema de coordenadas e parâmetros geométricos, dessa forma, tem-se:

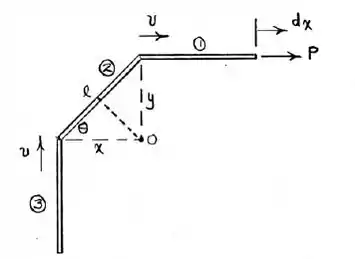
A partir do triângulo retângulo formado, pode-se relacionar as variáveis X e Y da seguinte forma:

x ²   +   y ²   =   l ²

Em termos diferenciais, teríamos:

x d x   +   y d y   =   0  

Para θ = 45°

x   =   y       p o r t a n t o           d x   =   - d y

Passo 2

A avaliação das parcelas das energias de forma diferencial é expressa por:

d U ’   =   d T   +   d V g

Para o exercício, é necessária a avaliação nos 3 pontos destacados no esboço dinâmico, portanto, cada componente energética estará sujeita a três quantificações.

d U ’   =   P * d x

d T   =   d   ( T 1   +   T 2   +   T 3 )

d T   = d m v 2 2 +   I o ω 2 2 + m v 2 2

d T   =   2 * m * V d V   +   I o   ω d ω

d T   =   2   m * a   * d x   + m * l 2 3 * a l √ 2 * d x l √ 2  

d T   =   8 3   m * a * d x

Passo 3

Para a energia potencial:

d V g =   d   ( V g 1   +   V g 2   +   V g 3 )

d V g = 0 + m * g * d x 2 + m * g * d x

d V g =   3 2   m * g * d x

Passo 4

Aplicando na equação geral do balanço energético, tem-se:

d U ’   =   d T   +   d V g

P * d x =   8 3   m * a * d x +   3 2   m * g * d x

Isolando a aceleração, tem-se que:

a =   3 8 P m -   3 g 2

Resposta

A expressão para a aceleração resultante da análise das parcelas energéticas é dada por:

a =   3 8 P m -   3 g 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um homem com massa de 90k g está sentado em uma cadeira da roda-gigante, a qual, excluindo-se o homem tem massa de 7500k g e raio de giração k O = 11,1m . Se um torque M = 120 10 3N ⋅ m é aplicado em
Um homem com massa de 75k g está agachado na extremidade do trampolim, como mostra a figura. Nessa posição, o raio de giração em relação a seu centro de gravidade é k G = 0,36m . Enquanto mantém sua p
A bobina tem massa de 75k g e raio de giração k O = 0,675m . Se uma corda é enrolada em torno de seu miolo interno e sua extremidade é puxada com uma força horizontal P = 200N , determine a velocidade
O tambor tem massa de 50k g e raio de giração em relação ao pino em O , k O = 0,23m . Partindo do repouso, o bloco suspenso B , de 15k g , é deixado cair por 3m , sem que se aplique o freio A C D . De
O disco semicircular uniforme de 15 kg é sustentado, na posição de equilíbrio mostrada, pelos dois cabos que estão enrolados em volta de seus cubos anexos e são guiados até as molas idênticas. Cada mo