Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 4.3 - Ex. 22
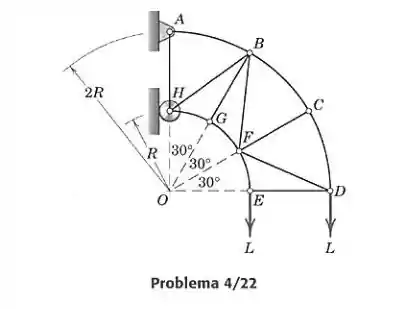
Determine a força no elemento da treliça carregada.
Passo 1
Vamos resolver as equações de equilíbrio em e para cada nó começando em . As forças positivas indicam tração e as negativas compressão, e sempre trataremos as forças desconhecidas como tração. Devemos olhar as barras curvas como se fossem retilíneas.
Nó E:
O triângulo é isósceles, então os ângulos e são iguais a:
Então temos:
Substituindo na expressão de :
Passo 2
Nó D:
Sabemos que o ângulo é igual a . Agora precisamos do ângulo . Vamos dar uma olhada melhor no triângulo :
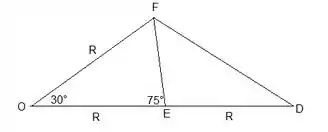
Vamos fazer a lei dos cossenos no tiângulo com os lados e e o ângulo de para achar o lado :
Agora, fazemos a lei dos senos, usando os lados e e seus ângulos opostos, e :
Agora usamos a relação fundamental trigonométrica para achar :
Passo 3
Agora aplicamos as equações de equilíbrio para :
Substituímos agora :
Com o falor de achamos :
Passo 4
Nó C:
É fácil aqui perceber que a inclinação de com a horizontal é de . Temos então:
Substituímos pelo valor achado na primeira equação:
Agora podemos ir para o nó para encontrar o valor de .
Passo 5
Nó F:
Vamos dar uma olhada melhor nas forças atuando em :
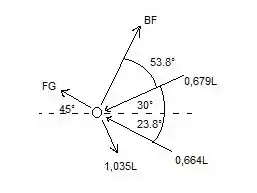
Colocamos na imagem o ângulo igual . O ângulo entre e a horizontal é:
Então agora podemos podemos calcular as equações pra achar :
Substituindo os cossenos e os valores das forças:
Agora para as forças verticais:
Substituindo os senos e os valores das forças:
Agora substituímos pelo valor encontrado na primeira equação: