Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 7ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 7º - Capítulo 6.Problemas - Ex. 25
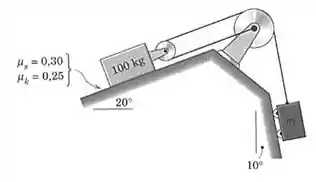
6/24) Determine a faixa das massas para o qual o bloco de está em equilíbrio . Todas as polias e roldanas têm atrito desprezível .
Passo 1
Então galera , seja a força peso do carrinho de massa .
Sendo assim , aplicando a equação de equilíbrio do carrinho em relação ao eixo :
Para o bloco de , por sua vez , temos que :
:
Passo 2
Assumindo que o movimento tende para baixo no plano inclinado , temos que :
A força máxima de atrito estático , por sua vez , é dada por :
Sendo assim , obtemos que :
Passo 3
Por outro lado , assumindo que o movimento tende para baixo no plano inclinado ,temos que :
De forma análoga ao passo anterior :
Consequentemente , o intervalo admissível é :
Resposta
Tranquilo pessoal? Então partiu resolver mais questões
Exercícios de Livros Relacionados
134- O macaco mostrado é projetado para levantar carros pequenos. O parafuso é rosqueado na bucha articulada em B e o eixo gira em um mancal de apoio em A . A rosca tem um diâmetro médio de 10m m e um
140- O pequeno rolamento na extremidade superior da barra uniforme está apoiado contra a superfície vertical em A , enquanto a extremidade arredondada B repousa sobre a plataforma que está ligeirament
139- Faça um gráfico da força P necessária para mover o caixote de 100k g para cima do plano com inclinação de 10 ° , a partir do repouso, para vários valores de x , desde zero até 10m . Determine o m
137- O bloco de 8k g está em repouso sobre o plano inclinado a 20 , com um coeficiente de atrito estático μ s = 0.50 . Determine a força horizontal mínima P que fará com que o bloco deslize.
138- O semicilindro com massa específica uniforme se apóia sobre uma superfície horizontal e está sujeito a uma força P aplicada como mostrado. Se P aumenta lentamente e é mantida normal a superfície