Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.10 - Ex. 134
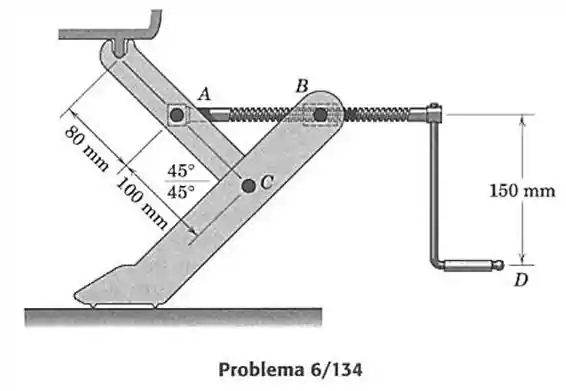
134- O macaco mostrado é projetado para levantar carros pequenos. O parafuso é rosqueado na bucha articulada em e o eixo gira em um mancal de apoio em . A rosca tem um diâmetro médio de e um passo (avanço por revolução) de . O coeficiente de atrito para as roscas vale . Determine a força normal a manopla em necessária para levantar uma massa de desde a posição mostrada e para abaixar a carga a partir da mesma posição. Despreze o atrito no pivô e no mancal em .
Passo 1
Antes de calcular o momento necessário para subir ou descer essa massa nós precisamos saber qual a força que se encontra axialmente no parafuso. Para isso vamos precisar da figura abaixo.
Onde é a força no parafuso e o ponto apresenta uma reação a todo esse sistema de forças, como não nos interessa essa reação vamos calcular a somatória dos momentos em para encontrar a força . Para isso vamos fazer a nossa viga equivalente abaixo que será possível calcular essa força:
é o peso da massa.
Onde apenas rebati o eixo todo em e em com o objetivo de encontrar a contribuição de momento de cada força:
Com essa expressão encontramos:
Passo 2
Agora que já encontramos a força axial no parafuso podemos anotar os dados do parafuso.
Avanço :
Raio :
Ângulo de atrito (em graus) para :
Ângulo de hélice (em graus):
Passo 3
Para subir a massa precisamos apertar o parafuso e para isso temos a fórmula (para :
Onde empregamos uma força em um eixo de logo o momento no parafuso será de:
A força para subir a massa será de:
E o momento para descer a massa:
O que nos dará uma força igual a:
Resposta
Para subir:
Para descer: