Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 11.Problemas - Ex. 31

Se as molas em A e C têm comprimento livre de 250 mm, enquanto a mola em B tem comprimento livre de 300 mm, determine a altura h da plataforma quando o sistema está em equilíbrio. Investigue a estabilidade dessa configuração de equilíbrio. O pacote a plataforma têm um peso total de 750 N.

Passo 1

Desenhando o diagrama do corpo livre:

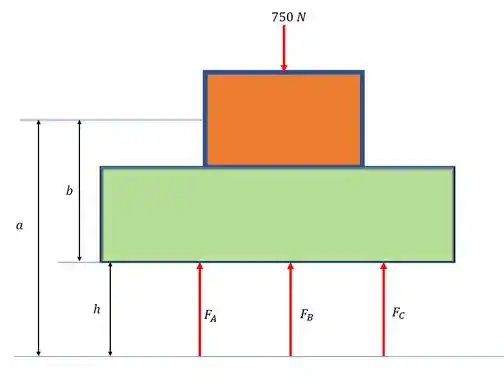
Passo 2

Podemos começar escrevendo a expressão da energia potencial gravitacional do peso do sistema W:

V g = W a

Como a = ( h + b ) Então:

V g = W h + b V g = 750 ( b + h )

Passo 3

Agora, vamos calcular a energia potencial armazenada pela mola:

V e = 1 2 k s 2 C a l c u l a n d o   o s   elongamentos das molas:

s = s - s 0

s A = 0,25 - h s B = 0,3 - h S C = 0,25 - h

Passo 4

Dados:

k 1 = 4 k N m = 4000 N m k 2 = 46 k N m = 6000 N m k 3 = 4 k N m = 4000 N m

Calculamos a energia potencial armazenada pelas molas:

V e = 1 2 k 1 s 2 + 1 2 k 2 s 2 + 1 2 k 3 s 2 V e = 1 2 ⋅ 4000 0,25 - h 2 + 1 2 ⋅ 6000 0,3 - h 2 + 1 2 ⋅ 4000 0,25 - h 2 V e = 2000 0,0625 - 0,5 h + h 2 + 3000 0,09 - 0,6 h + h 2 + 2000 0,0625 - 0,5 h + h 2 V e = 125 + 270 + 2000 - 1000 h - 1800 h - 1000 h + 7000 h 2 V e = 7000 h 2 - 3800 h + 520 J

Passo 5

Calculando a energia potencial total do sistema:

V = V g + V e V = 750 b + h + 7000 h 2 - 3800 h + 520 V = 750 b + 750 h + 7000 h 2 - 3800 h + 520

Passo 6

Para calcular a posição de equilíbrio, devemos calcular a primeira derivada de V:

d V d h = 0 d V d h = d d h 750 b + 750 h + 7000 h 2 - 3800 h + 520 d V d h = 14000 h + 750 - 3800 d V d h = 14000 h - 3050 d V d h = 0 ⇒ 14000 h - 3050 = 0   ⇒ 3050 14000 = 0,218   m

Passo 7

Agora vamos verificar a estabilidade do sistema. Para isso precisamos calcular a segunda derivada de V e = 7000 h 2 - 3800 h + 520 J:

d 2 V d h 2 = d d h 14000 h - 3050 = 14000 > 0 ⇒ e s t á v e l  

Resposta

A altura da plataforma é h = 0,218   m e o sistema é estável

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma mesa de servir uniforme com 5 kg é apoiada em cada lado por pares de ligações idênticas , AB e CD, e molas CE. Se a tigela tem uma massa de 1 kg, determine o ângulo θ onde a mesa está em equilíbri
O cone homogêneo tem uma cavidade cônica cortada, conforme a figura. Determine a profundidade d da cavidade em termos de h de modo que o cone se equilibre sobre o pivô e permaneça em equilíbrio indife
A montagem mostrada consiste em um bloco semicilíndrico e retangular. Se o bloco pesa 40 N e o semicilindro 10 N, investigue a estabilidade quando a montagem estiver apoiada na posição de equilíbrio.
Um bloco homogêneo repousa no topo da superfície cilíndrica. Derive a relação entre o raio do cilindro, r, e a dimensão do bloco b, para o equilíbrio estável. Dica: estabeleça a função energia potenci
Determine a altura h do cone em termos do raio r do hemisfério , de modo que o conjunto esteja em equilíbrio indiferente. Tanto o cone como o hemisfério são feitos do mesmo material.