Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.3 - Ex. 31

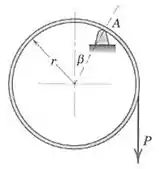
6/31) Um anel de metal com espessura desprezível tem massa m e raio médio r e está pendurado em A . Se o coeficiente de atrito entre o anel e o suporte é μ , determine a força vertical P aplicada à periferia do anel necessária para fazer o anel deslizar no suporte . Determine também o ângulo β no qual ocorre deslizamento .

Passo 1

Então galera , a primeira coisa que devemos fazer é aplicar a equação de equílibrio do sistema em relação ao eixo x :

∑ F x = 0   :

N sen ⁡ β - μ N cos ⁡ β = 0

Sendo assim , podemos obter uma relação trigonométrica para β , dada por :

tan ⁡ β = μ  

Logo ,

β = tan - 1 ⁡ μ

Passo 2

Bom pessoal , seja A o ponto de contato entre o suporte e o anel . Dessa forma , aplicando a equação de equilíbrio do momento em relação ao ponto A , temos que :

∑ M A = 0

P r - r sen ⁡ β - m g r sen ⁡ β = 0

Logo ,

P = m g sen ⁡ β 1 - sen ⁡ β  

Agora , como sabemos que :

β = tan - 1 ⁡ μ

sen ⁡ β = sen ⁡ ( tan - 1 ⁡ μ )

Logo , devemos lembrar da relação trigonométrica que nos diz que :

sen ⁡ ( arctan ⁡ x ) = x 1 + x 2

Portanto ,

sen ⁡ β = sen ⁡ ( tan - 1 ⁡ μ ) = μ 1 + μ 2

Substituindo sen ⁡ β pelo valor encontrado , obtemos que :

P = m g μ 1 + μ 2 - μ

Resposta

β = tan - 1 ⁡ μ

P = m g μ 1 + μ 2 - μ

Suave galera? Então bora próxima!!!

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Três pacotes de 4 kg, A, B e C são colocados em uma esteira transportadora que está em repouso. Entre a esteira e os pacotes A e C, os coeficientes de atrito são μ s = 0,3 e μ k = 0,2 ; entre o pacote
O cilindro mostrado na figura tem peso W e raio r. Expresse, em termos de W e r, a intensidae do maior binário M que pode ser aplicado ao cilindro para que ele não gire, considerando que o coeficiente
Um armário de 540 N é montado sobre rodízios que podem ser travados para se evitar seu rolamento. O coeficiente de atrito estático entre o piso e cada rodízio é 0,3. Considerando que os rodízios A e B
O cilindro mostrado na figura tem peso W e raio r, e o coeficiente de atrito estático μ s é o mesmo em A e B. Determine a intensidade do maior binário M que pode ser aplicado ao cilindro para que ele
Um armário de 540 N é montado sobre rodízios que podem ser travados para se evitar seu rolamento. O coeficiente de atrito estático entre o piso e cada rodízio é 0,3. Se h = 800m m , determine a intens