Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.5 - Ex. 113
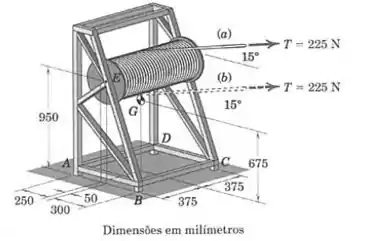
A estrutura é usada para armazenar e desenrolar cabos. A massa combinada da estrutura e do cabo é com centro de massa em . Determine as forças normais nos quatro pés (, , e ) se (a) o cabo sai pela parte de cima do carretel e (b) o cabo sai pela parte de baixo do carretel. Note que, em ambos os casos, o cabo sai do carretel em seu ponto médio horizontal. O raio efetivo do carretel é de .
Passo 1
O primeiro passo para simplificar esse problema é perceber que existe uma simetria muito importante nesse sistema:
Isso já facilita bastante! Temos apenas duas variáveis desconhecidas ( e ) e duas conhecidas: a força no carretel e o peso .
Passo 2
(a) Nesse caso vamos substituir a força que sai pela parte de cima do carretel como uma única força atuando no centro do carretel e um binário .
E agora vamos tratar o problema como se fosse bidimensional. Vamos montar uma equação de equilíbrio para o momento em torno do ponto (que no caso bidimensional, a vista “de lado” também está sobre o ponto ).
E então a força tem momento nulo, e ficamos apenas com a força , a força e o peso. Vamos desenhar as forças aqui, e conferir as distâncias no desenho do enunciado:
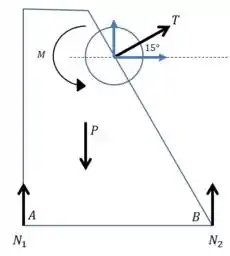
E essa força é o dobro das duas forças e , então:
Passo 3
E agora, ainda tratando do caso (a), vamos aplicar a condição de equilíbrio das forças na direção vertical para encontrar :
E então:
Passo 4
(b) Agora vamos fazer uma coisa bem parecida para o segundo caso.
Mais uma vez, vamos tratar a força como se estivesse atuando no centro, mas dessa vez acompanhada por um binário no sentido contrário:
E agora vamos só copiar as equações que montamos antes, mas trocando o sinal do binário.
Usando ficamos com o seguinte (já com o sinal do trocado):
E na equação do equilíbrio das forças não temos o binário, mas muda o valor de :
Resposta
(a) e .
(b) e .