Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 8.Problemas - Ex. 15
Um armário de 540 N é montado sobre rodízios que podem ser travados para se evitar seu rolamento. O coeficiente de atrito estático entre o piso e cada rodízio é 0,3. Se , determine a intensidade da força necessária para o movimento iminente do armário para a direita se todos os rodízios estiverem travados, se os rodízios em B estiverem travados e os rodízios em A estiverem livres para rodar, se os rodízios em A estiverem travados e os rodízios em B estiverem livres para rodar.
Passo 1
Beleza! Vamos começar esse excercício desenhando o DCL do armário para o caso mais geral, então, temos:
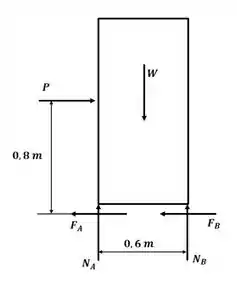
Então, vamos primeiro calcular a força P para que o armário tombe, quando isso acontecer, não haverão forças de apoio em A, então:
Dessa forma, calculando o somatório de momento em relação a B nesse caso:
Agora, para a letra considerando todos os rodízios travados, calculando o somatório de forças na direção :
As forças de atrito são dadas por:
Somando essas duas equações, temos:
Substituindo o valor encontrado de :
Agora, calculando o somatório de forças na direção :
Substituindo o valor encontrado de :
Então, como , o armário não tomba e fica na iminência de se mover para .
Passo 2
Agora para a letra onde os rodízios em A não estão travados temos:
Agora, calculando o somatório de forças na direção :
Agora calculando o somatório de momento em relação ao ponto A:
Substituindo os valores conhecidos, temos:
Então, como , o armário não tomba e fica na iminência de se mover para .
Passo 3
Agora para a letra onde os rodízios em B não estão travados temos:
Agora, calculando o somatório de forças na direção :
Agora calculando o somatório de momento em relação ao ponto B:
Substituindo os valores conhecidos, temos:
Então, como , o armário não tomba e fica na iminência de se mover para .