Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 7ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 7º - Capítulo 6.Problemas - Ex. 42
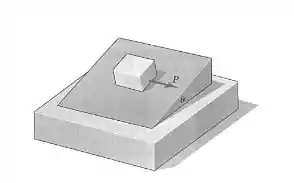
6/41) Um bloco uniforme de massa está em repouso para uma inclinação . Determine a força máxima que pode ser aplicada no bloco no sentido mostrado , antes que ocorra deslizamento .O coeficiente de atrito estático entre o bloco e o plano inclinado é . Determine também o ângulo entre adireção horizontal de e a direção do movimento inicial do bloco .
Passo 1
Bom galera , como já estamos acostumados , teremos que aplicar as equações de equilíbrio para resolvermos este exercício . Neste caso , será necessário aplicar as equações em relação aos três eixos :
Além disso , reparem que podemos encontrar a força de atrito de duas formas distintas :
Da forma tradicional :
Obtendo o módulo da força de atrito em cada uma das direções :
Logo , temos que :
Passo 2
Então pessoal , como visto no passo anterior :
Dessa forma , subtituindo esses valores na equação obtida anteriormente , temos que :
Sendo assim ,
Isolando , obtemos que :
Passo 3
Então galera, devemos lembrar que , como foi exposto neste capítulo e demonstrado em exercícios anteriores , deve ser maior que , caso contrário o bloco desliza mesmo sem a ação da força .
Sendo assim , temos que :
Resposta
De boa galera? Então bora resolver mais exercícios como esse!