Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 8.Problemas - Ex. 26

Um bloco de concreto de 500 N é elevado por um par de pinças mostrado na figura. Determine o menor valor admissível do coeficiente de atrito estático entre o bloco e as pinças em F e G.

Passo 1

Beleza! Vamos começar esse excercício desenhando o DCL para o braço superior:

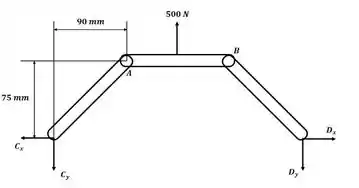
Devido a simetria do carregamento e do braço superior, temos:

C y = D y = 250   N

Agora, podemos usar semelhança de triângulos entre as forças no ponto C e a distância da haste esquerda da seguinte forma:

C x 90 = C y 75 → C x 90 = 250 75 → C x = 300   N

Passo 2

Agora podemos aplicar o somatório de forças na direção x :

+ → ∑ F x = 0

D x - C x = 0 → D x = 300   N

Passo 3

Agora vamos desenhar o DCL do braço inferior esquerdo, sendo assim:

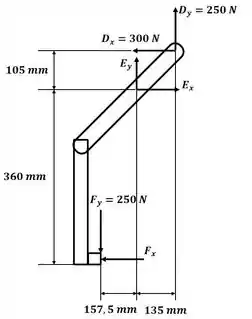
Agora vamos aplicar o somatório de momento em relação ao ponto E:

+ ↺ ∑ M E = 0

300 0,105 + 250 0,135 + 250 0,1575 - F x 0,36 = 0

Isolando F x e resolvendo:

F x = 290,6   N

Agora, sabemos que a força de atrito é dada por:

F = μ s N

E, nesse caso, temos F = F y e N = F x , então substituindo esses valores na fórmula:

F y = μ s F x → 250 = μ s 290,6 → μ s = 0,86

Resposta

μ s = 0,86

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

138- O semicilindro com massa específica uniforme se apóia sobre uma superfície horizontal e está sujeito a uma força P aplicada como mostrado. Se P aumenta lentamente e é mantida normal a superfície
Um cilindro de massa 250k g deve ser suportado pela corda que envolve o cano. Determine a maior força vertical F que pode ser aplicada à corda sem mover o cilindro. A corda passa (a) uma vez pelo cano
O barco tem um peso de 2500N( ≈ 250k g ) e é mantido na posição lateral de um navio pelas vergas em A e B . Um homem com um peso de 650N( ≈ 65k g ) entra no barco, enrola uma corda em torno de uma lan
Um cilindro de massa 250k g deve ser suportado pela corda que envolve o cano. Determine a menor força vertical F necessária para suportar a carga se a corda passa (a) uma vez pelo cano, β = 180 ° e (b
Os blocos A e B pesam 375N cada, e D pesa 150N . Usando os coeficientes de atrito estático indicados, determine a força de atrito entre os blocos A e B e entre o bloco A e o piso C .