Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 7ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 7º - Capítulo 5.Problemas - Ex. 97

91- A área sombreada é limitada por meio ciclo de uma onda senoidal e pelo eixo da onda. Determine o volume gerado por uma revolução completa da área em torno do eixo x .

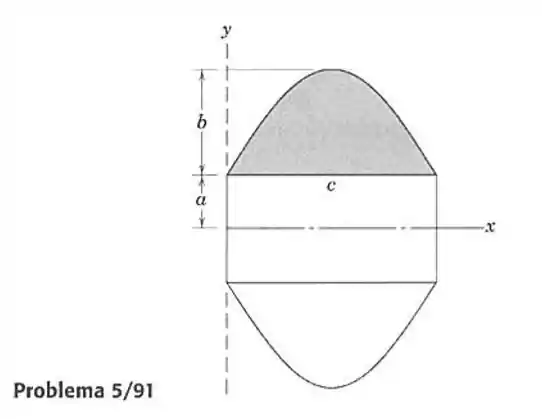
Passo 1

Pelo teorema de Pappus temos que o volume causado por uma área rotacionada em torno do eixo x é de:

V = 2 π y - A

Então precisamos calcular antes a área dessa figura e depois sua coordenada vertical do centroide.

E antes disso tudo precisamos saber sua função. Que tem a cara:

y = a + b s e n π c x

Onde a é o cruzamento da função com o eixo y , b   sua amplitude e π / x é a velocidade angular dessa função seno.

Passo 2

Calculando a área da função seno temos:

Comprimento da Linha vertical (função seno menos a reta y = a ):

L = a + b   s e n π c x

A = ∫ 0 c b   s e n π c x d x = - b c cos ⁡ π c π 0 c = 2 b c π

Encontramos essa integral por substituição.

Passo 3

Agora calculando ∫ y m   d A :

Onde y m é a média aritmética das funções onde elas estão compreendidas:

y m = 1 2 a + a + b s e n π x c = a + b 2 s e n π x c

Logo:

∫ y m d A = 1 2 ∫ 0 c a + b 2 s e n π x c b   s e n π x c d x

∫ y m d A = ∫ 0 c ( a b   s e n π x c + b 2 2 s e n 2 π x c )   d x

Como:

s e n 2 x + cos 2 ⁡ x = 1

E

cos 2 ⁡ x - s e n 2 x = cos ⁡ 2 x

Logo:

s e n 2 x = 1 2 - cos ⁡ 2 x 2

Então a integral fica:

∫ y m d A = ∫ 0 c a b s e n π x c d x + b 2 4 ∫ 0 c   d x - b 2 4 ∫ 0 c cos ⁡ 2 π x c   d x

A integral nos dá:

- a b c π cos ⁡ π x c 0 c + c b 2 4 - - b c 2 16 π sin ⁡ 2 π x c 0 c

2 a b c π + c b 2 4 = b c 2 a π + b 4  

Logo y - será:

y - = ∫ y m d A ∫ d A = b c 2 a π + b 4 2 b c π = a + b π 8

Passo 4

Agora podemos calcular o volume:

V = 2 π a + b π 8 2 b c π

V = 4 b c a + b π 8

Resposta

V = 4 b c a + b π 8

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O corpo mostrado em seção transversal é uma grande arruela de Neoprene. Calcule sua área superficial A e seu volume V.
A seção transversal monstrada representa um corpo de revolução, em torno do eixo z , de uma peça fabricada em ferro fundido. Calcule sua massa m .
Determine a área A da superfície curva A B C D do sólido de revolução mostrado.
Localize o centro de massa da casca homogênea, em formato de sino, de espessura uniforme, mas desprezível.
A caixa d’água elevada tem um topo cônico e fundo hemisférico e é fabricada usando placa de aço fina. Determine quantos metros quadrados de placa são necessários para fabricar a caixa d’água.