Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.3 - Ex. 42

6/42) A viga em uniforme , de massa é apoiada em suas extremidades sobre dois trilhos horizontais fixos como mostrado . Determine a força horizontal máxima que pode ser aplicada sem fazer com que a viga deslize , e encontre o valor da força de atrito correspondente em . O coeficiente de atrito estático entre a viga e os trilhos é . Considere , também ,

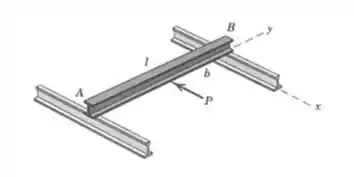
Passo 1

Então galera , como de costume , assumiremos equilíbrio do sistema .

Sendo assim ,aplicando a equação de equilíbrio do momento no ponto em relação ao eixo , obtemos que :

:

Logo ,

Da mesma forma , a equação de equilíbrio da viga em relação ao eixo é dada por :

Portanto ,

Passo 2

Bom pessoal , analisando as equações de e , obtemos que , para :

Sendo assim , a viga desliza primeiro em .

Sabendo disso , vamos calcular a força de atrito em através da relação :

Consequentemente ,

Isolando na equação , obtemos que :

Logo ,

Resposta

Tranquilo pessoal? Então partiu resolver mais questões

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma alavanca de peso desprezível é montada com folga em um eixo de 30m m de raio mostrado na figura. Sabendo que a aplicação da força P de intensidade 275N irá justamente iniciar a rotação no sentido

O binário M B é aplicado no giro do tambor motriz para manter a velocidade constante da cinta de polimento mostrada na figura. Sabendo que μ k = 0,45 entre a cinta e o bloco de 15k g , inicia o polime

Um base máquina de 900k g é rolada ao longo de um piso de concreto usando uma série de tubos de aços com diâmetro externo de 100m m . Sabendo que o coeficiente de resistência ao rolamente é 0,5m m ent

O elo de ligação mostrado na figura é usado frequentemente na construção de pontes de rodovias para possibilitar a expansão causada por variações de temperatura. Em cada um dos pinos A e B de 60m m ,

Uma enceradeira elétrica de 225N é operada sobre uma superficie cujo coeficiente de atrito cinético é 0,25 . Considerando que a força normal por unidade de área entre o disco e o assoalho é distríbuid