Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 7.4 - Ex. 60
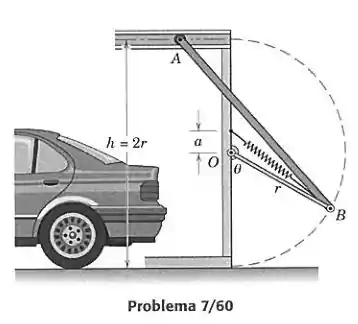
A porta de garagem uniforme mostrada em seção tem uma massa e está equipada com dois mecanismos acionados por mola iguais ao mostrado, um de cada lado da porta. O braço tem massa desprezível e o canto superior da porta é livre para se mover horizontalmente sobre um rolete. O comprimento não esticado da mola é de forma que na posição superior com a força da mola vale zero. Para garantir um funcionamento suave da porta quando ela atinge a posição vertical fechada em , é desejável que ela seja insensível a movimentos nessa posição. Determine a rigidez da mola necessária para esse projeto.
Passo 1
Dizer que na posição vertical fechada da porta ela é insensível a movimentos é a mesma coisa que dizer que a porta está num equilíbrio estável. Se temos uma função potencial para a energia potencial do sistema em função da angulação da porta, a condição para o equilíbrio é:
Temos também a relação que garante o equilíbrio estável:
Devemos então achar a função potencial do sistema em função de , para então derivar e aplicar as condições para o equilíbrio estável.
Passo 2
A energia potencial do sistema é composta pela energia das duas molas e a energia potencial gravitacional da porta. Vamos começar com as molas. Queremos saber o elongamento da mola em função de , para então aplicar a fórmula para a energia potencial das molas:
Temos na figura o seguinte triângulo:
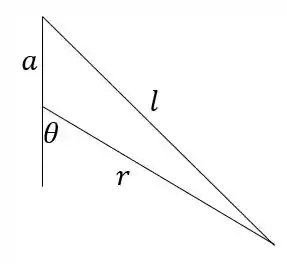
Para achar o comprimento total de cada mola, podemos usar a lei dos cossenos:
Então:
Se o comprimento da mola relaxada é , então o elongamento é:
Com o valor de , calculamos então a energia potencial elástica:
Passo 3
Agora falta calcular a energia potencial gravitacional . Ela é função da altura do centro de massa da porta em relação ao ponto . Vamos definir como referencial de energia potencial gravitacional igual a zero, ou seja, se . Então:
Temos então que achar esse valor de .
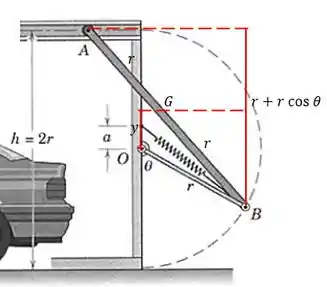
A distância vertical de até é . Então a altura de em relação a deve ser a metade, igual a . Então a altura de em relação a vai ser:
A expressão para a energia potencial gravitacional é então:
Passo 4
Somando e , achamos a energia potencial total do sistema:
Vamos calcular a primeira e a segunda derivadas em relação a , que são as funções que devemos analisar para a estabilidade:
Esse valor é de fato igual a zero para . Vamos então derivar novamente:
Para , nossa expressão é reduzida a:
A estabilidade requer que a segunda derivada seja positiva. Então encontramos o valor máximo de :