Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 7ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 7º - Capítulo 6.Problemas - Ex. 51

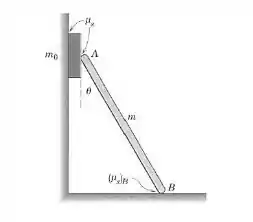
6/47) Um bloco de massa m 0 é colocado entre a parede vertical e a extremidade superior , A , da barra esbelta uniforme de massa m . Se o coeficiente de atrito estático entre o bloco e a parede e também entre o bloco e a barra vale μ s , determine a expressão geral parao valor mínimo , θ m í n , do ângulo θ para o qual o bloco permanecerá em equilíbrio . Avalie sua expressão para as condições μ s = 0,5 e

(a) m m 0 = 0,1

(b) m m 0 = 1 , e

(c) m m 0 = 10 .

Para cada caso , especifique ocoeficiente de atrito estático mínimo μ s B   necessário para evitar escorregamento em B .

Passo 1

Então galera , nós sabemos que para impedir o deslizamento do bloco , a força de atrito em ambas faces deve atingir o valor máximo .

Agora , como de costume , aplicaremos as equações de equiilíbrio que conhecemos ao bloco e a barra . Sendo assim , temos que :

Bloco :

∑ F = 0   : 2 μ S N A - m 0 g = 0     ,   N A = m 0 g 2 μ s     ( 1 )

Barra :

∑ M B = 0   : m g l 2 sen ⁡ θ + μ s N A l sen ⁡ θ - N A l cos ⁡ θ = 0   ( 2 )

Combinando as equações (1) e (2) e resolvendo o sistema linear associado a elas , achamos que :

m g l 2 sen ⁡ θ + μ s m 0 g 2 μ s   l sen ⁡ θ - m 0 g 2 μ s   l cos ⁡ θ = 0

Logo ,

θ = tan - 1 ⁡ 1 μ s 1 + m m 0 = θ m i n

Passo 2

Bom pessoal , aplicando a equação de equilíbrio da barra em relação ao eixo x , temos que :

Barra :

∑ F = 0   : N B - m g - μ s N A = 0  

N B = m g + μ s m 0 g 2 μ s = m + m 0 2 g

Logo ,

μ s B = F B N B = m 0 g 2 μ s m + m 0 2 g = 1 μ s 1 + 2 m m 0

Passo 3

Agora tudo fica mais fácil! Basta substituirmos os dados fornecidos por cada item nas equações obtidas nos passos anteriores :

(a) m m 0 = 0,1   :

  θ m i n = tan - 1 ⁡ 1 0,5 1 + 0,1 = 61,2 °  

μ s B = 1 0,5 1 + ( 2 * 0,1 ) = 1,667

( μ s > 1 resultado muito comum apesar de ser possível )

(b) m m 0 = 1   :

θ m i n = tan - 1 ⁡ 1 0,5 1 + 1 = 45 °  

μ s B = 1 0,5 1 + ( 2 * 1 ) = 0,667

(c) m m 0 = 10   :   θ m i n = 10,3 °   ,   μ s B = 0,0952  

θ m i n = tan - 1 ⁡ 1 0,5 1 + 10 = 10,3 °  

μ s B = 1 0,5 1 + ( 2 * 10 ) = 0,0952

Resposta

m m 0 = 0,1   :   θ m i n = 61,2 °   ,   μ s B = 1,667

m m 0 = 1   :     θ m i n = 45 °   μ s B = 0,667

m m 0 = 10   :   θ m i n = 10,3 °   ,   μ s B = 0,0952  

E aí , Topam resolver mais questões com a gente ?

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma haste delgada de comprimento L está apoiada entre um pino C e uma parede vertical e sustenta uma carga P em sua extremidade A. Sabendo que o coeficiente de atrito estático é 0,20 em B e C, calcule
Um eixo excêntrico de 100 mm de raio mostrado na figura é usado para controlar o movimento da placa CD. Sabendo que o coeficiente de atrito estático entre o excêntrico e a placa é 0,45, e desprezando
No Problema 8.30, determine o intervalo de intensidade dos valores da força vertical P aplicada em E para a qual a placa se moverá para baixo.
A placa ABCD de 225 N é ligada em A e D aos colares que podem deslizar sobre a barra vertical. Sabendo que o coeficiente de atrito estático entre os colares e a barra é 0,40, determine se a placa está
Resolva o Problema 8.32 considerando que o diâmetro do tubo é 30 mm.