Uma haste delgada de comprimento L está apoiada entre um pino C e uma parede vertical e sustenta uma carga P em sua extremidade A. Sabendo que o coeficiente de atrito estático é 0,20 em B e C, calcule o intervalo de valores da razão para que o equilíbrio seja mantido.
Passo 1
Tá legal! Vamos começar esse excercício desenhando o DCL para a haste
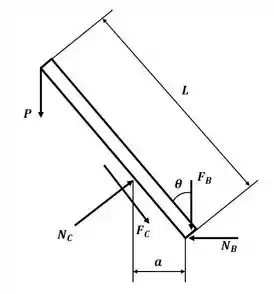
Sabemos que as forças de atrito nos pontos B e C podem ser escritas como:
Passo 2
Agora vamos aplicar o somatório de momento em relação ao ponto B:
Essa será a equação 1. Agora vamos aplicar o somatório de forças na direção :
Essa será nossa equação 2. Agora aplicando o somatório de forças na direção :
Essa será nossa equação 3.
Passo 3
Agora para resolver esse sistema de equações, vamos multiplicar a equação 2 por e subtrair essa expressão da equação 3:
Colocando os termos em evidência:
Agora vamos substituir o valor de encontrado na equação 1:
Isolando :
Substituindo os valores de e :
Agora, assumindo que a tendência da haste é se mover para baixo, resolvendo da mesma maneira, chegaremos na mesma equação para , só com os sinais trocados, então fazendo :
Então, o intervalo para deve ser: