Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 8.Problemas - Ex. 30
A placa ABCD de 225 N é ligada em A e D aos colares que podem deslizar sobre a barra vertical. Sabendo que o coeficiente de atrito estático entre os colares e a barra é 0,40, determine se a placa está em equilíbrio na posição mostrada na figura quando a intensidade da força vertical aplicada em E é , .
Passo 1
Tá legal! Vamos começar esse excercício desenhando o DCL para a placa:
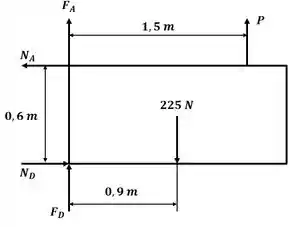
Sabemos que as forças de atrito nos pontos A e D podem ser escritas como:
Passo 2
Vamos analisar primeiro a condição da letra com . Agora vamos aplicar o somatório de momento em relação ao ponto D:
Agora vamos aplicar o somatório de forças na direção :
Agora aplicando o somatório de forças na direção :
Agora vamos calcular a força de atrito estático máxima para o sistema, calculando em A e D, temos:
Então, a força de atrito máxima é:
Dessa forma, como então a placa está em equilíbrio e não se move.
Passo 3
Vamos analisar a segunda condição, a letra com . Agora vamos aplicar o somatório de momento em relação ao ponto D:
Agora vamos aplicar o somatório de forças na direção :
Agora aplicando o somatório de forças na direção :
Agora vamos calcular a força de atrito estático máxima para o sistema, calculando em A e D, temos:
Então, a força de atrito máxima é:
Dessa forma, como então a placa está se movendo.