Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 8.Problemas - Ex. 31
No Problema 8.30, determine o intervalo de intensidade dos valores da força vertical P aplicada em E para a qual a placa se moverá para baixo.
Passo 1
Tá legal! Vamos começar esse excercício desenhando o DCL para a placa:
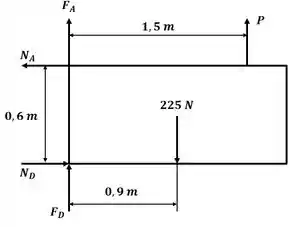
Sabemos que as forças de atrito nos pontos A e D podem ser escritas como:
Passo 2
Conforme vimos no Problema 8.30, cada uma das forças de atrito máxima para é de 135 N, então, devemos analisar duas faixas de força separadamente, a primeira sendo de e a segunda de . Vamos começar com o primeiro caso e vamos aplicar o somatório de momento em relação ao ponto D:
Agora vamos aplicar o somatório de forças na direção :
Agora aplicando o somatório de forças na direção :
Agora vamos calcular a força de atrito estático máxima para o sistema, calculando em A e D, temos:
Então, a força de atrito máxima é:
Dessa forma, a placa irá se mover se , então, calculando essa expressão:
Passo 3
Vamos analisar a segunda condição, para . Agora vamos aplicar o somatório de momento em relação ao ponto D:
Agora vamos aplicar o somatório de forças na direção :
Agora aplicando o somatório de forças na direção :
Agora vamos calcular a força de atrito estático máxima para o sistema, calculando em A e D, temos:
Então, a força de atrito máxima é:
Dessa forma, a placa irá se mover se , então, calculando essa expressão:
Então, a placa vai se mover se estiver no intervalo: