Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 8.Problemas - Ex. 33
Resolva o Problema 8.32 considerando que o diâmetro do tubo é 30 mm.
Passo 1
Tá legal! Vamos começar esse excercício desenhando o DCL para a parte superior da chave:
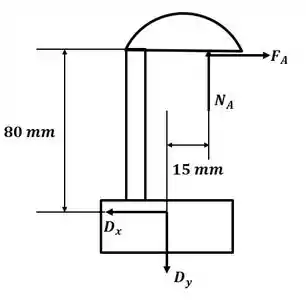
Sabemos que a força de atrito no ponto A pode ser escrita como:
Passo 2
Agora vamos aplicar o somatório de momento em relação ao ponto D:
Agora vamos aplicar o somatório de forças na direção :
Agora vamos analisar o DCL do tubo:
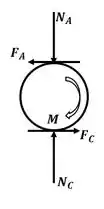
Aplicando o somatório de forças na direção :
Passo 3
Agora vamos desenhar o diagrama de corpo livre para o braço da chave:
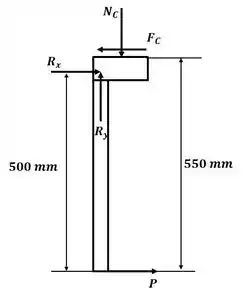
E vamos aplicar o somatório de momento em relação ao ponto F:
Substituindo o valor de encontrado no passo 2:
E, substituindo o valor de encontado no passo 2:
Simplificando o termo da expressão e resolvendo, temos:
Resposta
Exercícios de Livros Relacionados
Os blocos A e B têm uma massa de 7k g e 10k g , respectivamente. Usando os coeficientes de atrito estático indicados, determine a maior força vertical P que pode ser aplciada à corda sem causar movime
O bloco A tem uma massa de 50k g e se apoia sobre a superfície B para a qual μ s = 0,25 . Se o coeficiente de atrito estático entre a corda e o pino fixo em C é μ s ' = 0,3 , determine a maior massa d
O bloco A tem uma massa de 50k g e se apoia sobre a superfície B para a qual μ s = 0,25 . Se a massa do cilindro suspenso D é 4k g , determine a força de atrito que atua sobre A e verifique se ocorre
8.6. O homem de 90k g sobe pela escada e para na posição mostrada após sentir que a escada está na iminência do deslizamento. Determine o coeficiente de atrito estático entre a plataforma de atrito em
8.2. Determine a força P mínima exigida para empurrar a caixa deslize plano acima. A caixa tem massa de 50k g e o coeficiente de atrito entre a caixa e o plano é μ s = 0,25