Um eixo excêntrico de 100 mm de raio mostrado na figura é usado para controlar o movimento da placa CD. Sabendo que o coeficiente de atrito estático entre o excêntrico e a placa é 0,45, e desprezando o atrito dos rolos de suporte, determine a força P necessária para manter o movimento da placa, sabendo que a placa tem 20 mm de espessura, a maior espessura da placa para a qual o mecanismo é autotravante (ou seja, para que a placa não possa mover por maior que seja a força P).
Passo 1
Beleza! Vamos começar esse excercício desenhando o DCL para o eixo:
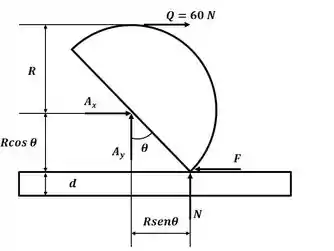
Agora vamos aplicar o somatório de momento em relação ao ponto A, sabendo que :
Isolando da equação, temos:
Passo 2
Agora vamos desenhar o diagrama de corpo livre para a placa:
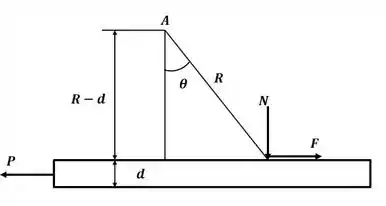
Fazendo o somatório de forças na direção :
Agora, para encontrar o valor do ângulo para a letra iremos usar o DCL anterior e um pouco de trigonometria, fazendo:
Substituindo os valores de e para a letra :
Agora podemos voltar à equação do passo 1 e calcular a reação normal:
E, agora, substituindo esse valor na relação encontrada para :
Passo 3
Agora, para a letra , vamos olhar novamente para a equação da força P:
Nesse caso, como P é muito grande, N também será muito grande, e para que isso seja verdade olhando para a equação da reação normal:
Então, o denominador dessa equação deve ser zero, sendo assim:
Substituindo o valor de dado no enunciado:
E, finalmente, olhando para a equação encontrada no passo 2:
Substituindo esse valor de :