Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 8.Problemas - Ex. 123
Resolva o Problema considerando que o tambor esticador esteja fixo e não possa girar.
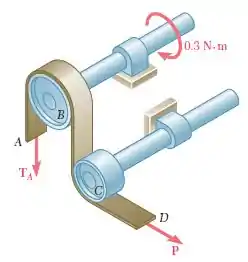
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
O primeiro a se fazer é desenhar o diagrama do tambor de acionamento:
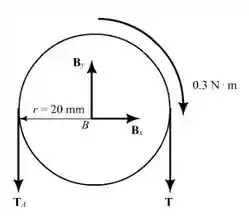
Podemos fazer também o diagrama do tambor tensor :
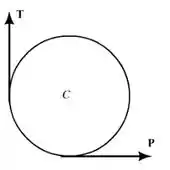
Passo 2
Fazendo o momento de equilíbrio no ponto do respectivo tambor, temos que:
Portanto:
Determinaremos agora, o menor valor admissível de considerando que o tambor esticador esteja fixo e não possa girar:
Logo:
Passo 3
Portanto, se o tambor é fixo, a fita deve escorregar no sentido-anti-horário. Temos que:
Resposta
Exercícios de Livros Relacionados
98. Determine a força horizontal necessária para se mover um automóvel de 11250N com pneus de 580m m de diâmetro ao longo de uma estrada horizontal com velocidade constante. Despreze todas as formas d
103. Uma corda A B C D está amarrada em dois canos, como mostra a figura. Sabendo que o coeficiente de atrito estático é 0,25 , determine (a) o maior valor da massa m para a qual o equilíbrio é possív
102. Uma corda A B C D está amarrada em dois canos, como mostra a figura. Sabendo que o coeficiente de atrito estático é 0,25 , determine (a) o menor valor da massa m para a qual o equilíbrio é possív
105. O coeficiente de atrito estático μ s entre o blocoB e a superfície horizontal e entre a corda e o suporte C é 0,40 . Sabendo que m A = 12k g , determine o menor massa do bloco B para que o equilí
104. Um bloco de 1350N é sustentado por uma corda enrolada 1 1 2 volta em torno de uma barra horizontal. Sabendo que o coeficiente de atrito estático entre a corda e a barra é 0,15 , determine a faixa