Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 14ª Edição - Russel C. Hibbeler- Ed: 14º - Capítulo 5.Problemas - Ex. 68
67. Devido a uma distribuição desigual do combustível nos tanques da asa, os centros de gravidade da fuselagem e das asas e são localizados como mostra a figura. Se essas componentes possuem pesos , e , determine as reações normais das rodas e sobre o solo.
Passo 1
Como o enunciado pede as forças normais nas rodas, então só estamos interessados em saber a componente vertical que age em cada roda.
Para isso basta utilizar as equações de equilíbrio do momento referente aos eixos e e usar a equação de equilíbrio referente as forças na direção .
Abaixo tem um diagrama das forças que atuam no sistema.
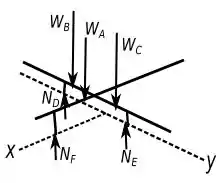
Passo 2
Vamos utilizar as equações de equilíbrio agora.
Mas como na primeira equação obtemos , logo:
Logo:
Resposta
Exercícios de Livros Relacionados
92- Dois rolos de fitas são presos a um eixo e segurados por mancais em A e D . O raio do rolo B é 30m m e o raio do rolo C é 40m m . Sabendo que T B = 80N e o sistema gira em velocidade constante, de
93- Resolva o Problema 4.92 , considerando que o rolo C é trocado por um rolo de raio 50m m
94- Duas correias de transmissão passam por duas roldanas soldadas a um eixo apoiado por mancais em B e D . A roldana em A tem um raio de 60m m , e a roldana em C tem um raio de 50m m . Sabendo que o
118- Resolva o Problema 4.117 , considerando que o cabo E F é substituído por um cabo preso aos pontos E e H .
95- Uma alavanca de 200m m e uma polia de diâmetro de 240m m estão soldadas ao eixo B E que é suportado pelos mancais em C e D . Se a carga vertical de 720N é aplicada em A quando a alavanca está na h