Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.10 - Ex. 130

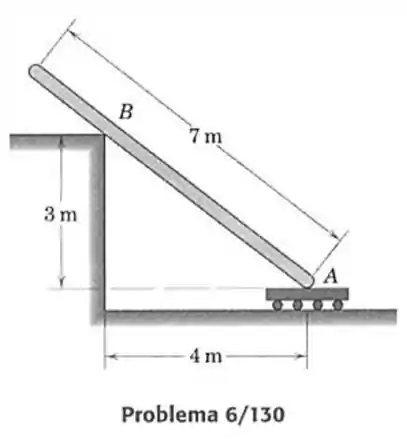
130- A extremidade inferior A da prancha uniforme de 80   k g se apoia em roletes que estão livres para se mover na superfície horizontal. Se os coeficientes de atrito estático e dinâmico entre a prancha e o vértice B valem 0.80 e 0.70 , respectivamente, calcule a força de atrito F atuando em B se a prancha é solta a partir do repouso na posição mostrada.

Passo 1

O sistema de forças na prancha será:

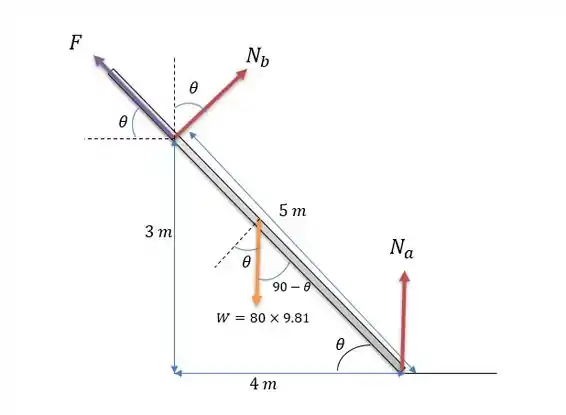
Onde temos as normais em B que é N b e a normal em A que é N a e apenas uma força de atrito em B que é a F .

Se fizermos a somatória dos momentos em A nós iremos encontrar:

N b × 5 - 80 × 9.8 1 cos ⁡ θ × 3.5 = 0

Onde 3.5   m é a posição na barra onde se encontra o seu peso e a força de atrito não gera momento, e :

cos ⁡ θ = 4 5

sin ⁡ θ = 3 5

Logo:

N b = 125.568   N

Passo 2

Fazendo a somatória das forças verticais nós temos:

N b sin ⁡ θ = F × cos ⁡ θ

Resolvendo essa igualdade nós encontramos:

F = N b × sin ⁡ θ cos ⁡ θ = 94.176   N

Passo 3

Agora devemos encontrar o coeficiente de atrito em B e garantir se nosso sistema está estático ou não, por que senão está o cálculo estará errado:

F = μ × N

μ B = F N = 94.176 125.568 = 0.75

Então o sistema ainda encontra-se estático pois o atrito encontrado é menor que o atrito dinâmico, logo a força de atrito F será:

F = 94.176   N

Resposta

F = 94.176   N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A magnitude da força P é aumentada lentamente. A caixa homogênea de massa m desliza ou tomba primeiro? Indique o valor de P que causaria cada ocorrência. Negligencie qualquer efeito do tamanho dos pés
A força 700N é aplicada ao bloco de 100k g , que fica estacionário antes de a força ser aplicada. Determine a magnitude e a direção da força de atrito F exercida pela superfície horizontal no bloco.
Determine o coeficiente mínimo de atrito estático μ s que permitirá que o tambor com cubo interno fixo seja enrolado na inclinação de 15 ° a uma velocidade constante sem escorregar. Quais são os valor
Os coeficientes de atrito estático e cinético entre o bloco de 100k g e o plano inclinado são 0,30 e 0,20 , respectivamente. Determine a a força de atrito F atuando no bloco quando P é aplicado com um
A ilustração mostra o projeto de um dispositivo de travamento do tipo came, que, na presença de atrito suficiente, limita o movimento do corpo B para ser apenas para a esquerda; o movimento para a dir