Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 7.5 - Ex. 77

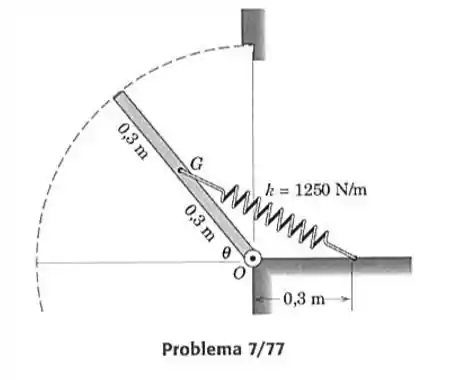
77- A figura mostra a vista lateral de uma janela de ventilação de 10   k g e centro de massa em G , articulada em relação a um eixo horizontal que passa por sua aresta em O . Quando θ = 90 , a mola de rigidez k = 1250   N / m não está alongada. Calcule a energia potencial total da janela e da mola em função de θ , e faça um gráfico de θ = 0 até θ = 90 . A partir do gráfico, especifique a posição e equilíbrio diferente daquela em θ = ± 90 e verifique sua condição de estabilidade. Você pode justificar o fato do equilíbrio em θ = + 90 ser estável com a mola e ser instável sem a mola?

Passo 1

Vamos desenhar o mecanismo para θ = 90 para descobrirmos qual o comprimento natural da mola ( l 0 ) .

Por Pitágoras temos:

l 0 = 0.3 2 + 0.3 2 = 0.424   m

Agora rotacionando a mola em um ângulo θ em relação a horizontal:

Para conseguirmos calcular o comprimento final dessa mola basta olharmos para o triângulo formado entre os catetos h e ( d + 0.3 ) . E para calcular essas duas variáveis faltantes vamos fazer.

cos ⁡ θ = d 0.3 → d = 0.3 cos ⁡ θ

sin ⁡ θ = h 0.3 → h = 0.3 sin ⁡ θ

Logo o comprimento l f será por Ptiágora:

l f 2 = ( 0.3 cos ⁡ θ + 0.3 ) 2 + ( 0.3 sin ⁡ θ ) 2

l f 2 = 0.3 2 cos 2 ⁡ θ + 0.18 cos ⁡ θ + 0.3 2 + 0.3 2 sin 2 ⁡ θ

l f 2 = 0.18 + 0.18 cos ⁡ θ

l f 2 = 0.18 ( 1 + cos ⁡ θ )

l f = 0.424 1 + c o s θ

Logo a variação do comprimento da mola (alongamento) será de:

Δ x = l f - l 0

Δ x = 0.424 1 + cos ⁡ θ - 0.424 = 0.424 ( 1 + cos ⁡ θ   - 1 )

O que nos dá uma energia potencial elástica igual a:

V e = 1 2 k Δ x 2

V e = 1 2 1250 0.424 1 + cos ⁡ θ   - 1 2

V e = 112.36 ( 1 + c o s θ - 1 2

Passo 2

A energia potencial gravitacional por tabela já foi feita, uma vez que o rebatimento da posição do centro de gravidade na vertical é representada pela altura h que é:

h = 0.3 sin ⁡ θ

E o peso da barra W é:

W = m g = 10 × 9.81 = 98.1   N

Logo a energia potencial gravitacional será:

V g = m g h = 98.1 × 0.3 sin ⁡ θ = 29.43 sin ⁡ θ

Passo 3

A energia total V do sistema será:

V = 112.36 ( 1 + c o s θ - 1 2 + 29.43 sin ⁡ θ

Plotando o gráfico no intervalo de θ indo de 0 até 90 dessa função nós iremos ter:

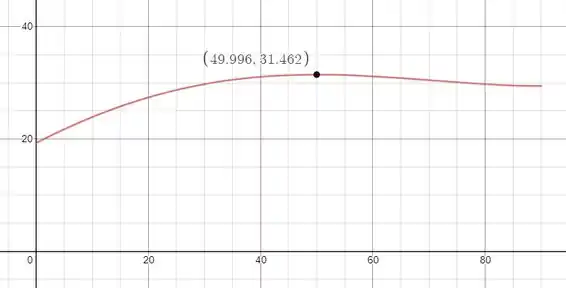
Um ponto de máximo loca em θ = 49.996 com energia V valendo 31.462   J e por ser máximo local esse ponto é um ponto de instabilidade do sistema.

Se expandirmos nosso intervalo conseguimos ver que temos pontos de mínimo local em θ = ± 90 o que configura posições de estabilidade em nossa derivada segunda.

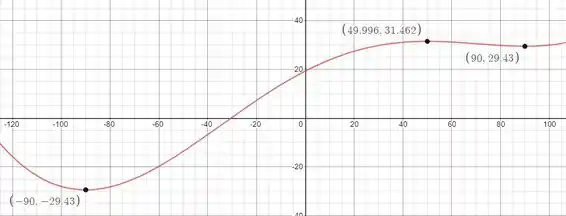
Passo 4

Sem a mola a energia do sistema seria somente.

V = 29.43 sin ⁡ θ

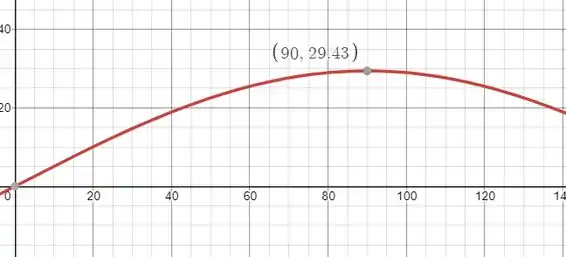
E a posição de θ = 90 estaria em um ponto de máximo local o que seria uma posição de instabilidade.

Resposta

Passo 3 e 4 .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A figura mostra a seção transversal de um recipiente composto por uma casca hemisférica de raio r e uma casca cilíndrica de altura h , feitas do mesmo material. Especifique o limite de h para haver es
A casca semicilíndrica de raio r gira em torno de um eixo, pelos pontos O , como mostrado. A massa das duas hastes de suporte é pequena comparada à massa da casca. Determine o valor máximo de h para o
Um bloco retangular uniforme de altura h e massa m está centrado em uma posição horizontal, sobre a superfície circular fixa de raio r . Determine o valor limite de h para haver estabilidade.
Determine os valores de equilíbrio de θ e a estabilidade do equilíbrio em cada posição para a roda não balanceada sobre a rampa de 10°. O atrito estático é suficiente para prevenir deslizamento. O cen
Determine a intensidade da força P exigida para manter a barra lisa de 50 kg em equilíbrio com θ = 60 ° .