Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 16.Problemas - Ex. 124

A polia A gira com a velocidade angular e aceleração angular mostradas. Determine a aceleração angular do bloco E no instante mostrado.

Passo 1

Começaremos o exercício encontrando a velocidade linear no ponto C e a velocidade angular da polia B com o auxílio do diagrama a seguir:

v C = ω A r A = 40 0,05 → v C = 2   m / s

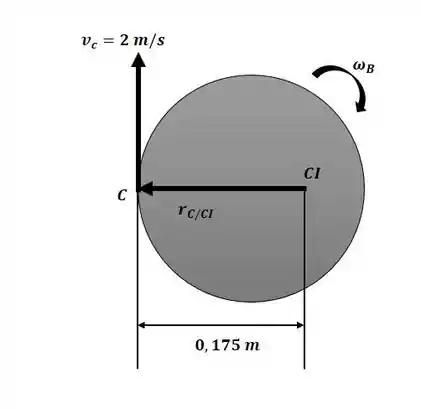
Agora iremos encontrar a velocidade angular da polia B

ω B = v C r C / C I = 2 0,175 → ω B = 11,43   r a d / s

Passo 2

Agora iremos encontrar a aceleração tangencial da polia A com base na aceleração angular fornecida:

a C t = α A r A = 5 0,05 → a C t = 0,25   m / s 2

Agora iremos aplicar a equação da aceleração entre os pontos C e D com o auxílio do diagrama a seguir:

a → D = a → C + α B × r → D / C - ω B 2 r → D / C

a D n i → = a C n i → + 0,25 j → + α B k → × 0,175 i → - 11,43 2 0,175 i →

a D n i → = a C n - 22,86 i → + ( 0,25 - 0,175 α B B ) j →

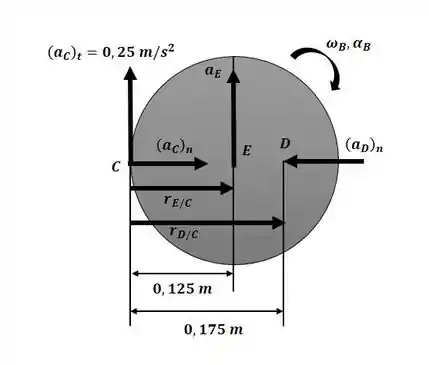
Agora igualando a componente j:

0 = 0,25 - 0,175 α B → α B = 1,43   r a d / s 2

Passo 3

Agora iremos aplicar a equação da aceleração para os pontos C e E:

a → E = a → C + α B × r → E / C - ω B 2 r → E / C

a E j → = a C n i → + 0,25 j → + - 1,43 k → × 0,125 i → - 11,43 2 0,125 i →

a E j → = a C n - 16,33 i → + 0,0714 j →

Igualando a componente j, temos:

a E = 0,0714   m / s 2

Resposta

a E = 0,0714   m / s 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O volante com raio de 18 pol. Está rigidamente preso a um volante de 1,5 pol. - eixo de raio que pode rolar ao longo de trilhos paralelos. Sabendo que no instante mostrado o centro do eixo tem uma vel
No sistema de engrenagens planetárias mostrado, o raio das engrenagens A, B, C e D é de 3 pol. E o raio da engrenagem externa E é de 9 pol. Sabendo que a engrenagem A tem uma velocidade angular consta
O disco mostrado tem uma velocidade angular constante de 500 rpm no sentido anti-horário. Sabendo que a haste BD tem 250 mm de comprimento, determine a aceleração do colar .D quando (a) θ = 90 ∘ , ( b
No compressor de ar de dois cilindros mostrado, as bielas BD e BE têm cada uma 190 mm de comprimento e a manivela AB gira em torno do Ponto fixo A com uma velocidade angular constante de 1500 rpm no s
O braço AB tem uma velocidade angular constante de 16 rad / s no sentido anti-horário. No instante em que θ = 0 , determine a aceleração (a) do colar D, (b) do ponto médio G da barra BD.