Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 4.Problemas - Ex. 96
Resolva o Problema , considerando que o eixo foi girado no sentido horário em seus mancais de e que a carga de permanece na vertical.
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
Para resolver este problema, vamos fazer análises com vetores nas três dimensões para facilitar a organização.
Temos o seguinte diagrama de corpo livre:
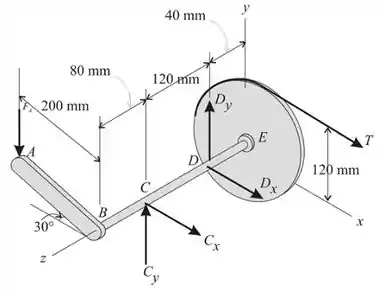
Passo 2
Vamos aplicar a condição de equilíbrio:
Resolvendo, temos que:
Agora é só igualar os coeficientes correspondentes. Temos que:
Logo:
Passo 3
Igualando os coeficientes de , temos que:
Logo:
Igualando os coeficientes de , temos que:
Logo:
Portanto, podemos dizer que:
Passo 4
Fazendo o somatório de forças em , temos:
Fazendo o somatório de forças em , temos:
Portanto, podemos dizer que:
Resposta
Exercícios de Livros Relacionados
Um anel uniforme de aço, com 600m m de diâmetro, tem uma massa de 50k g e está sustentado por três cabos, cada um com 500m m de comprimento, presos aos pontos A , B e C , como mostrado. Calcule a forç
A esfera lisa e homogênea repousa na caneleta de 120 ° e se apoia contra a placa que é normal à direção da canaleta. Determine o ângulo θ , medido a partir da horizontal, para o qual a reação em cada
A pequena escada em tripé é útil para apoiar uma extremidade de uma passarela. Se F representa o módulo da carga direcionada para baixo causada pela passarela (não mostrada), determine a reação em cad
O centro de massa da porta de 30k g está no centro do painel. Se o peso da porta é sustentado inteiramente pela dobradiça inferior A , calcule o módulo da força total suportada pela dobradiça em B .
O mastro de 9m tem uma massa de 600k g e tem centro de massa na metade do seu comprimento. Ele é apoiado por uma rótula em A e pelos dois cabos sob forças trativas T 1 e T 2 . O cabo que suporta a car