Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 14ª Edição - Russel C. Hibbeler- Ed: 14º - Capítulo 5.Problemas de Revisão - Ex. 3
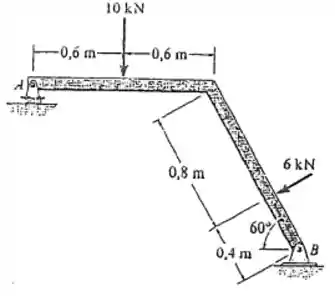
Determine a reação normal no rolete A e as componentes horizontal e vertical no pino B para o equilíbrio
Passo 1
Fala, meu querido!
Este é um problema de estática bem direto e basicamente vamos aplicar 3 equações da estática para achar as reações em A e B.
Essas 3 equações são o equilíbrio das forças em x e y; e a soma dos momentos em algum ponto qualquer da barra.
Passo 2
Bem estamos em equilíbrio então as forças verticais, horizontais e momentos se anulam
Aí a ideia aqui é a gente usar as equações de equilíbrio para achar as reações no rolete e no pino.
Nesse tipo de questão sempre devemos começar pelo diagrama de corpo livre:
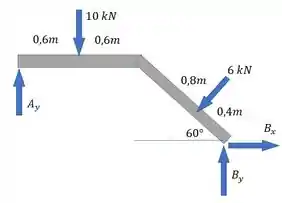
As forças do nosso problema já foram demarcadas, olha só que ótimo. Só o que precisamos pensar um pouquinho foi sobre os apoios. Só lembra que A é um rolete, então ele só faz força perpendicular à superfície.
Passo 3
A primeira coisa que vamos fazer aqui é o somatório dos momentos. Você pode fazer primeiro o somatório das forças em y, por exemplo, mas se aplicarmos a soma dos momentos em relação ao ponto B vamos achar de cara a força vertical atuante em A, então vamos lá!
Lembrando que o que gira no sentido horário é positivo e no anti-horário é negativo (isso é só uma convenção, você pode fazer ao contrário se preferir).
Vamos calcular o momento um a um.
Para :
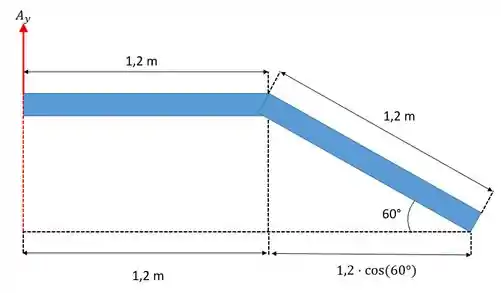
Assim o termo referente a será:
Agora para a força de
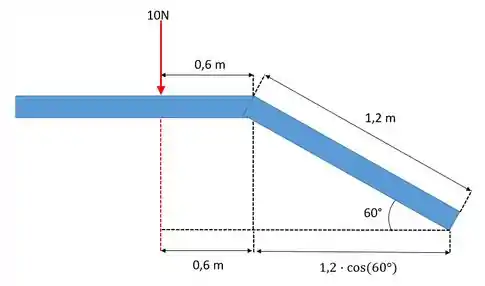
Assim o momento referente à força de vale:
E é negativo porque gira no sentido anti-horário.
Agora temos o último caso, da força de :
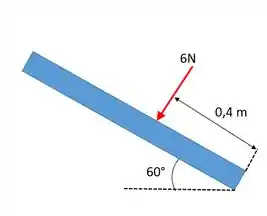
Repare que essa força já atua perpendicularmente à barra então não precisamos decompor nada =D. Fica assim:
Novamente o valor é negativo porque gira o barra no sentido anti-horário.
Passo 4
Agora vamos juntar todos esses momentos que acabamos de calcular e colocar juntos:
Repara que tivemos de decompor a parte inclinada da barra no eixo horizontal (x) para achar a distância (o braço de alavanca). Fizemos isso utilizando o
Passo 5
Agora vamos fazer o somatório das forças em x:
Aqui vamos ter que decompor a força de 6 newtons, para isso é importante que a gente veja onde estão os ângulos, olha só:
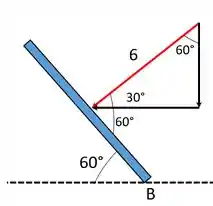
Com esses ângulos a gente vai poder achar os valores das componentes horizontal e vertical dessa força:
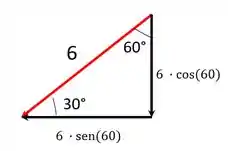
Aqui pegamos a componente horizontal da força de 6 newtons, para calcular essa componente foi só multiplicar pelo .
Finalmente para as forças em y:
De novo tivemos de decompor a força de 6 newtons, mas dessa vez na direção vertical então tivemos de utilizar o
Prontinho!