Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.10 - Ex. 176
Quatro forças são exercidas no olhal, como mostrado. Se o efeito resultante delas sobre o parafuso é um esforço trativo de na direção , determine os valores necessários de e .
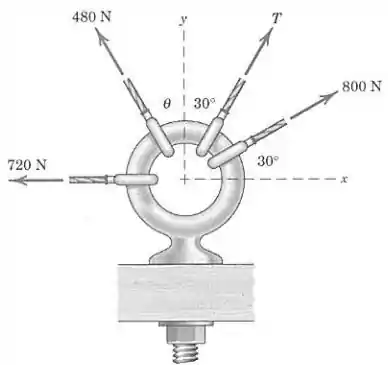
Passo 1
A resultante das forças em é , então:
Assim, obtivemos uma equação com duas incógnitas, e . Fazendo o somatório das forças em e igualando a zero, obteremos outra equação com as mesmas incógnitas:
Passo 2
Desse modo, formamos o seguinte sistema de duas equações e duas incógnitas:
Mesmo que tentássemos resolver o sistema eliminando a variável , chegaríamos a uma equação transcendental. Por isso, usamos um método numérico, por meio de um computador, para obter a seguinte solução:
Resposta
Exercícios de Livros Relacionados
80. Dois binários agem sobre a viga. Determine a intensidade de F de modo que o momento de binário resultante seja 450N ⋅ m anti-horário. Onde atua na viga o momento de binário resultante?
81. A corda passando por dois pinos A e B do quadro está sujeita a uma tração de 100N . Determine a tração P necessária que age sobre a corda que passa pelos pinos C e D de modo que o binário resultan
79. Se F = 200N , determine o ângulo θ necessário para que o momento de binário resultante seja zero.
85. Determine o momento de binário resultante que age sobre a viga. Resolva o problema de duas maneiras;(a) some os momentos em relação ao ponto O .
89. Dois binários agem sobre a estrutura. Se d = 1,2m , determine o momento de binário resultante. Calcule o resultado decompondo cada força em componentes x e y e(b)somando os momentos de todas as co