Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 8.Problemas - Ex. 145
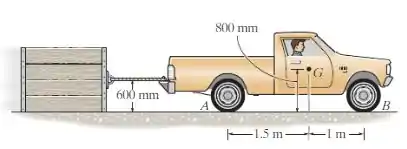
A caminhonete tem massa de e um centro de massa em . Determine a maior carga que ela pode puxar se (a) a caminhonete tem tração traseira enquanto as rodas dianteiras são livres para girar e (b) a caminhonete tem tração nas quatro rodas. O coeficiente de atrito estático entre as rodas e o solo é e entre a caixa e o solo é
Passo 1
De início, vamos dar uma olhada no diagrama de corpo livre para a letra (a) dessa questão para entendermos as forças que estão atuando.
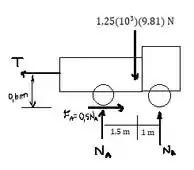
Passo 2
Quando nós temos um sistema em equilíbrio, o somatório das forças que atuam nesse sistema, em todos os eixos de referência ( é igual a zero. Vamos aplicar esse princípio na nossa questão! Adotando como direções positivas para cima e para direita, temos o seguinte:
Passo 3
O somatório dos momentos em relação a um ponto, para o sistema em equilíbrio, deve ser igual a zero. Vamos calcular o momento em relação ao ponto e, assumindo como sentido positivo o anti-horário, temos:
Passo 4
Como a carga se move, temos:
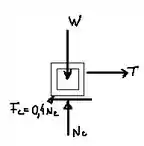
Vamos analisar o somatório as forças nessa situação. Quando nós temos um sistema em equilíbrio, o somatório das forças que atuam nesse sistema, em todos os eixos de referência ( é igual a zero. Vamos aplicar esse princípio na nossa questão! Adotando como direções positivas para cima e para direita, temos o seguinte
Passo 5
Agora vamos desenhar o diagrama de corpo livre para a letra (b) dessa questão.
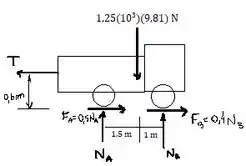
Passo 6
Agora temos tração nas rodas traseiras e dianteiras. Nesse caso, temos que e . O somatório dos momentos em relação a um ponto, para o sistema em equilíbrio, deve ser igual a zero. Vamos calcular o momento em relação aos pontos e e, assumindo como sentido positivo o anti-horário, temos:
Passo 7
Quando nós temos um sistema em equilíbrio, o somatório das forças que atuam nesse sistema, em todos os eixos de referência ( é igual a zero. Vamos aplicar esse princípio na nossa questão! Adotando como direções positivas para cima e para direita, temos o seguinte:
Temos um sistema de três equações com três incógnitas. Vamos resolvê-lo para encontrar os valores de , e !
Assim,
Passo 8
Como a carga se move, temos:
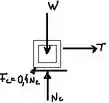
Vamos analisar o somatório as forças nessa situação. Quando nós temos um sistema em equilíbrio, o somatório das forças que atuam nesse sistema, em todos os eixos de referência ( é igual a zero. Vamos aplicar esse princípio na nossa questão! Adotando como direções positivas para cima e para direita, temos o seguinte
Resposta
- ;
- .