Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 7.10 - Ex. 87

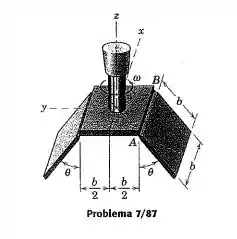
As abas quadradas uniformes, cada uma de massa m , são livremente articuladas em A e B à placa quadrada e o eixo associado, que giram em torno do eixo vertical z com uma velocidade angular constante ω . Determine a velocidade angular ω necessária para manter um ângulo positivo especifico θ .

Passo 1

Para resolvermos esse problema vamos precisar recordar o teorema dos eixos paralelos para encontrar a componente do tensor de inércia correspondente a um eixo coordenado geral, como também usaremos a definição de momento fletor para encontrarmos ω .

Passo 2

Temos que as forças aplicadas no sistema são a força peso e a normal, uma contrária a outra, porém em pontos diferentes da placa. Assim, temos que pela regra da mão direita, o momento fletor resultante será

∑ M x = I x y ⋅ ω z ˙ + I y z ⋅ ω z 2

Mas temos que ω z = c t e . Assim:

∑ M x = I y z ⋅ ω z 2

Agora precisamos calcular I y z , porém vemos que o seu eixo de rotação está em uma outra posição favorável para usarmos o teorema dos eixos paralelos. Dessa forma, temos que

I y z = I y ' z ' + m ⋅ r y → ⋅ r z →

Calculando então I y ' z ' , teremos que

∫ l ⋅ sin ⁡ θ ⋅ l ⋅ cos ⁡ θ ⋅ d m = 1 24 ⋅ m ⋅ b 2 ⋅ sin ⁡ 2 ⋅ θ

Vemos pelo esquema que r y → será a distância da origem do sistema até o fim da barra, logo:

r y → = - b 2 + b 2 ⋅ sin ⁡ θ ⋅ j →

E por consequência, r z → = - b 2 ⋅ cos ⁡ θ ⋅ k → . Substituindo então em I y z temos que

I y z = 1 24 ⋅ m ⋅ b 2 ⋅ sin ⁡ 2 ⋅ θ + m ⋅ - b 2 + b 2 ⋅ sin ⁡ θ ⋅ - b 2 ⋅ cos ⁡ θ

I y z = m ⋅ b 2 4 ⋅ 2 3 ⋅ sin ⁡ 2 ⋅ θ + cos ⁡ θ

Usando agora a relação de momento fletor, temos que

∑ M x = m ⋅ g ⋅ r 1 - m ⋅ g ⋅ r 2 = I y z ⋅ ω z 2

Onde r 1   e   r 2 são as distâncias até onde as forças estão sendo aplicadas. Continuando, temos que

m ⋅ g ⋅ b 2 + b 2 ⋅ sin ⁡ θ - m ⋅ g ⋅ b 2 = m ⋅ b 2 4 ⋅ 2 3 ⋅ sin ⁡ 2 ⋅ θ + cos ⁡ θ ⋅ ω z 2

g ⋅ tan ⁡ θ = b ⋅ 2 3 ⋅ sin ⁡ θ + 1 2 ⋅ ω 2

ω = 1 b ⋅ 6 ⋅ g ⋅ tan ⁡ θ 4 ⋅ sin ⁡ θ + 3

Resposta

ω = 1 b ⋅ 6 ⋅ g ⋅ tan ⁡ θ 4 ⋅ sin ⁡ θ + 3

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O volante de 50 kg tem um raio de giração em relação a seu centro de massa k O = 250m m . Ele gira com uma velocidade angular constante de 1200 rev/min antes de o freio ser aplicado. Se o coeficiente
A bobina de 200 kg tem um raio de giração em relação a seu centro de massa k G = 300m m . Se o momento de binário é aplicado à bobina e o coeficiente de atrito cinético entre a bobina e o solo é μ k =
O cilindro de 100 kg rola sem deslizar sobre o plano horizontal. Determine a aceleração de seu centro de massa e sua aceleração angular.
A barra fina uniforme de 60 kg está inicialmente em repouso sobre um plano horizontal liso quando as forças são aplicadas. Determine a aceleração do centro de massa da barra e a aceleração angular da
A barra fina de 12 kg está presa com pino ao rolete pequeno A que desliza livremente ao longo da ranhura. Se a barra é solta do repouso em θ = 0 ° , determine a aceleração angular da barra e a acelera