Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 17.Problemas fundamentais - Ex. 17

A bobina de 200 kg tem um raio de giração em relação a seu centro de massa k G = 300   m m . Se o momento de binário é aplicado à bobina e o coeficiente de atrito cinético entre a bobina e o solo é μ k = 0,2 , determine a aceleração angular da bobina, a aceleração de G e a tração no cabo.

Passo 1

Começaremos o exercício aplicando as equações de movimento para o sistema com o auxílio do diagrama a seguir:

+ ↑   ∑ F y = m a G y

N - 200 9,81 = 0 → N = 1962   N

+ →   ∑ F x = m a G x

T - 0,2 1962 = 200 a G

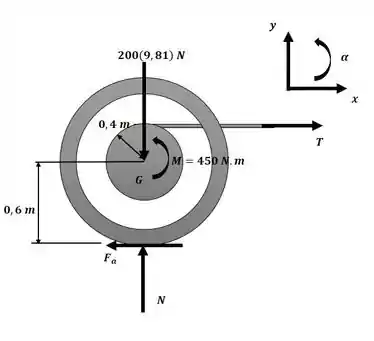
Essa será nossa equação número 1.

↺ +   ∑ M A = M k A

450 - 0,2 1962 1 = 18 α + 200 a G ( 0,4 )

Essa será nossa equação número 2.

Passo 2

Agora iremos aplicar a equação da aceleração vista no capítulo 16 para o ponto de ligação da corda:

a G = a A + α × r G / A - ω 2 r G / A

a G i = - a A j + α k × 0,4 j - ω 2 ( - 0,4 j )

a G i = 0,4 α i + 0,4 ω 2 - a A j

Igualando a componente i, temos:

a G = 0,4 α

Essa será nossa equação 3.

Passo 3

Agora iremos resolver o sistema de equações encontrado, substituindo a equação 3 na 2, temos:

450 - 0,2 1962 1 = 18 α + 200 a G ( 0,4 )

450 - 0,2 1962 1 = 18 α + 200 ( 0,4 α ) ( 0,4 )

α = 1,15   r a d / s 2

Substituindo esse valor na equação 3:

a G = 0,4 1,15 → a G = 0,461   m / s 2

E agora substituiremos esse valor na equação 1:

T - 0,2 1962 = 200 ( 0,4 α )

T - 0,2 1962 = 200 ( 0,4 ) ( 1,15 )

T = 485   N

Resposta

α = 1,15   r a d / s 2

a G = 0,461   m / s 2

T = 485   N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Se as rodas traseiras da empilhadeira fornecerem uma força de tração combinada de F A = 1500N , determine a sua aceleração e as reações normais sobre os pares de rodas traseiras e dianteiras. A empilh
A caixa uniforme tem uma massa de 50 kg e repousa sobre o carrinho tendo uma superfície inclinada. Determine a menor aceleração que vai fazer com que a caixa tombe ou deslize em relação ao carrinho. Q
O carro esportivo tem uma massa de 1,5 Mg e um centro de massa em G. Determine o tempo mais curto que ele leva para alcançar uma velocidade de 80 km/h, partindo do repouso, se o motor impulsiona somen
O carro, tendo uma massa de 1,40 Mg e centro de massa em G c , puxa um reboque carregado tendo uma massa de 0,8 Mg e centro de massa em G r . Determine as reações normais sobre ambas as rodas dianteir
O reboque com sua carga tem uma massa de 150 kg e um centro de massa em G. Se ele é submetido a uma força horizontal P = 600 N, determine a aceleração do reboque e a força normal sobre o par de rodas