Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.10 - Ex. 175

A ação combinada das três forças sobre a base em O pode ser obtida estabelecendo sua resultante passando por O . Determine os módulos de R e do momento M associado.

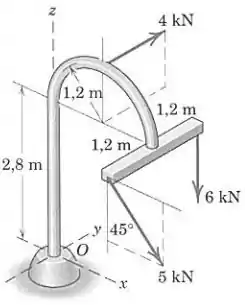
Passo 1

A resultante R das três forças é calculada assim:

R = 4   k N   j + 6   k N   - k + 5   k N   i cos ⁡ 45 ° - k   s e n   45 °

R = 3,5355   i + 4   j - 9,5355   k   k N

Então, o módulo R será:

R = 3,5355 2 + 4 2 + - 9,5355 2

R = 10,93   k N

Passo 2

Agora calculamos as componentes M x , M y e M z do momento M :

M x = 5   k N cos ⁡ 45 ° 1,2   m - 6   k N   1,2   m - 4   k N   2,8 + 1,2   m

M x = - 18,9574   k N ∙ m

M y = 5   k N cos ⁡ 45 ° 1,2 + 1,2   m + 5   k N   s e n   45 °   2,8   m + 6   k N   1,2 + 1,2   m

M y = 3 2 , 785   k N ∙ m

M z = 5   k N   s e n   45 °   1,2   m + 4   k N   1,2   m

M z = 9,0426   k N ∙ m

Então, o módulo M será:

M = - 18,9574 2 + 32,785 2 + 9,0426 2

M = 38,9   k N ∙ m

Resposta

R = 10,93   k N

M = 38,9   k N ∙ m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

91. Se M 1 = 500N ⋅ m , M 2 = 600N ⋅ m e M 3 = 450N ⋅ m , determine a intensidade e os ângulos de direção coordenados do momento de binário resultante.
Determine a intensidade necessária dos momentos de binário M 1 , M 2 e M 3 de modo que o momento de binário resultante seja M R → = - 300 i + 450 j - 600 kN ⋅ m .
94. Se a intensidade do momento de binário que age sobre a tubulação é 50N ⋅ m , determine a intensidade das forças de binário aplicadas em cada chave. A tubulação está no plano x - y .
93. Se F = 80N , determine a intensidade e os ângulos de direção coordenados do momento de binário. A tubulação se encontra no plano x - y .
Determine os ângulos de direção coordenados α , β , γ da força F em relação a O seja zero.