Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 2.Problemas - Ex. 183
A ação combinada das três forças sobre a base em pode ser obtida estabelecendo sua resultante passando por . Determine os módulos de e do momento associado.
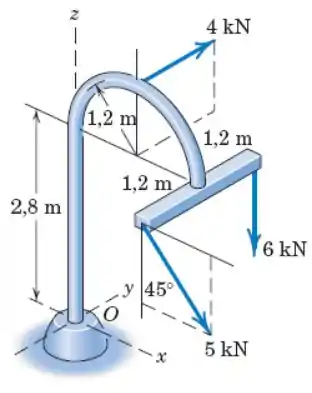
Passo 1
A resultante das três forças é calculada assim
Então, o módulo de será
Passo 2
Agora calculamos as componentes do momento
De forma análoga para
Por fim, para temos
Então, o módulo será
Pronto, tá resolvido nosso exercício.
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
176- Um bloco retangular de massa específica ρ 1 flutua em um líquido de massa específica ρ 2 . Determine a razão r = h / c , onde h é a altura submersa do bloco. Avalie r para um bloco de carvalho fl
174- Um béquer com água doce está em uma balança quando o peso de aço inoxidável de 1k g é colocado no béquer. Qual é a força normal que o peso exerce sobre o fundo do béquer? De quanto aumenta a leit
175- Especifique o módulo e a localização da força resultante que atua em cada lado e no fundo do aquário, devido a água doce dentro dele.
178- As duas cascas hemisféricas estão perfeitamente seladas sobre as suas superfícies de contato e o ar em seu interior foi parcialmente removido até que uma pressão de 14k P a foi atingida. A pressã
180- A água doce em um canal é contida pela placa uniforme de 2.5m , que pode bascular livremente em A . Se a comporta foi projetada para abrir quando a profundidade da água atingir 0.8m , como mostra