Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 2.Problemas - Ex. 176
Reduza o sistema de carregamento dado a um sistema força-binário no ponto Em seguida, determine a distância à direita do ponto na qual atua a resultante das três forças.
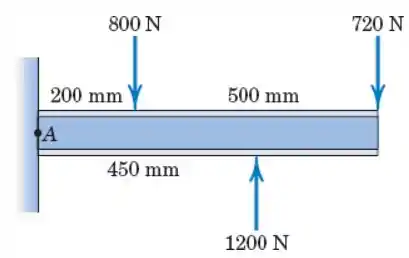
Passo 1
Todas as forças atuam na vertical, então, vamos considerar o sentido para baixo como positivo. Sendo assim, teremos
Agora, vamos somar os momentos causados por cada força em torno de , para calcular o momento total
Passo 2
Como a força resultante é para baixo, ela deve atuar a uma distância positiva de , a fim de produzir um momento resultante no sentido horário (negativo) em torno de
Porém, já obtivemos no passo anterior, logo
Passando para milímetros vamos ter
Pronto, tá resolvido nosso problema.
Resposta
Exercícios de Livros Relacionados
2.41. Determine a intensidade e a direção θ de F B , de modo que a força resultante seja direcionada ao longo do eixo y positivo e tenha uma intensidade de 1500N .
2.40. Determine a intensidade e a direção, medida no sentido anti-horário a partir do eixo x positivo, da força resultante das três forças que atuam sobre o anel A. Considere F 1 = 500N e θ = 20 ° .
2.39. Determine a intensidade de F 1 e sua direção θ, de modo que a força resultante seja direcionada verticalmente para cima e tenha a intensidade de 800N .
2.43. Se Φ = 30 ° e F 1 = 1,25k N , determine a intensidade da força resultante que atua sobre o suporte e sua direção, medida no sentido horário a partir do eixo x positivo.
2.37. Se a intensidade da força resultante que atua sobre a chapa precisa ser 6k N e sua direção no sentido horário do eixo x positivo é θ = 30 ° , determine a intensidade de F 2 e o ângulo Φ